Сильное напряжение разг: Напряжение Сил- Физических 6 Букв

нервотрёпка — это… Что такое нервотрёпка?

нервотрёпка — нервотрёпка …   Словарь употребления буквы Ё

НЕРВОТРЁПКА — НЕРВОТРЁПКА, и, жен. (разг.). Волнения, беспокойство. Ненужная н. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

нервотрёпка — ж. разг. 1. Обстановка, обстоятельства, условия, которые требуют нервного напряжения. 2. Состояние сильного нервного напряжения, вызванное такой обстановкой, такими обстоятельствами, условиями. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 …   Современный толковый словарь русского языка Ефремовой

нервотрёпка — нервотрёпка, и, род. п. мн. ч. пок …   Русский орфографический словарь

нервотрёпка — и; ж.; разг. Обстоятельства, условия, требующие нервного напряжения; вызванное ими состояние сильного напряжения нервов. Ненужная нервотрёпка. Нервотрёпка изматывает …   Словарь многих выражений

Нервотрёпка (фильм) — Нервотрёпка Nervous Ticks Жанр комедия Режиссёр Рокки Лэнг Автор сценария Дэвид Франкель …   Википедия

нервотрепка — НЕРВОТРЁПКА и; ж.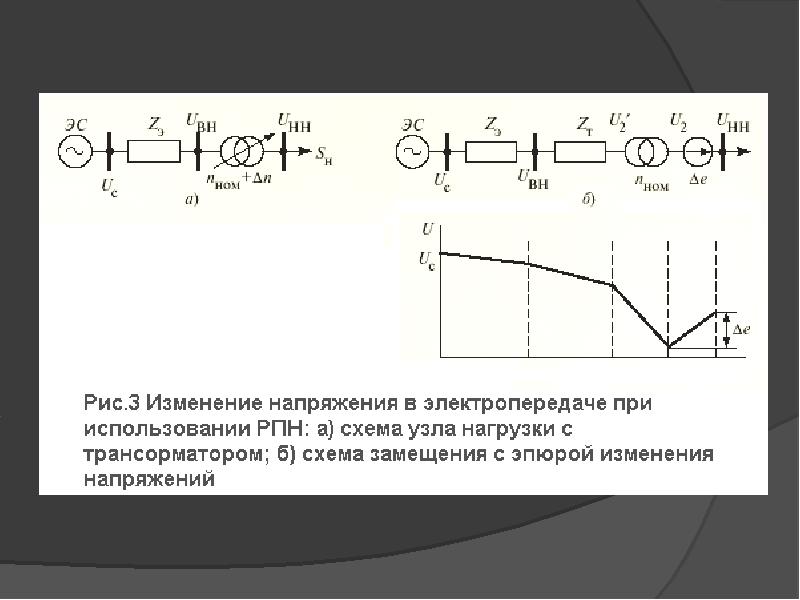 Разг. Обстоятельства, условия, требующие нервного напряжения; вызванное ими состояние сильного напряжения нервов. Ненужная н. Н. изматывает …   Энциклопедический словарь

Трепка — трёпка I ж. 1. процесс действия по гл. трепать I 2. 2. Результат такого действия; нагоняй, побои. II ж. разг. 1. процесс действия по гл. трепать II 2. Результат такого действия; сильная морская качка. III ж. разг. 1 …   Современный толковый словарь русского языка Ефремовой

нервотрепка — тревога, беспокойство, трепка нервов, волнение, треволнения, переживания, напряжение Словарь русских синонимов. нервотрепка см. переживания Словарь синонимов русского языка. Практический справочник. М.: Русский язык …   Словарь синонимов

Уолкер, Ким — В Википедии есть статьи о других людях с фамилией Уолкер. Ким Уолкер Kim Walker Имя при рождении …   Википедия

Значение, Определение, Предложения . Что такое напряг

Джек пошевелил пальцами ног, а потом поочередно напряг мышцы голеней, бедер, спины и плеч.

Я изогнул большой палец, сделал легкое движение остальными и резко напряг все мышцы руки.

Я напряг пальцы левой руки, и мне удалось продвинуть ее на несколько сантиметров к ноге.

Он напряг свои мощные задние ноги для отчаянного прыжка, но было поздно.

Малакар напряг свой арсенал рук и ног и подавил зевок.

Ты специально напряг бицепс, чтобы меня впечатлить?

Пуаро произнес это со значением, и Альфред снова напряг память.

– Я хочу, чтобы ты максимально напряг визуальную память.

С Рейнольдсом посложнее, он алкаш, да и с деньгам у него напряг.

Я напряг зрение, чтобы разглядеть ее, и издал торжествующий крик: это были сани, а на них хорошо знакомая мне уродливая фигура.

Я напряг зрение, но ничего не смог увидеть. Либо они носились слишком высоко, либо были невидимы, либо, подумал я, их не было там вовсе.

Я чувствую, как ты напряг свои извилины, Натаниэль.

В Кингстоне мы с мистером Уэллсом в очередной раз поменялись местами, и я напряг всю свою волю, чтобы как можно быстрее преодолеть последний участок пути до Ричмонда.

Ученый напряг зрение и увидел обычные уставленные книгами стеллажи, ячейки для хранения свитков и несколько столов для работы с архивными материалами.

И учитывая возраст девочек, невольно напряг.

Ты ведь создаешь напряг в наших отношениях. В будущем это может оказаться неполезно.

Лицо Шеффилда показалось мне знакомым, и я напряг память, вспоминая его досье.

У меня немного напряг со временем.

Ставь под вопрос все, что говорит Дедушка Напряг.

Слегка изменив положение ног, он напряг мышцы, потянул мешки, снова отпустил, ища полного равновесия и наилучших точек опоры для своего тела.

Но год выдался тяжёлый, и с деньгами напряг.

Я бы с удовольствием, но у меня со временем напряг, на работе дел невпроворот и еще дети…

Лэнгдон мгновенно толкнул Витторию за колонну и встал рядом с ней. Девушка направила пистолет в сторону звука. Американец напряг слух.

И плюс ко всему, есть небольшой напряг между мной и Левоном!

Он напряг мозги. Нужно очень-очень-очень счастливое воспоминание… такое, которое

Американец напряг слух, чтобы услышать, о чем идет речь, но в этот миг относительную тишину прорезал другой голос.

Так-то всё нормально, только с математикой напряг.

Система 1601 года была для доиндустриального общества, и массовый рост населения после промышленной революции напряг существующую систему.

Белые полосы отложили японскую часть своего мирового турне после того, как Джек напряг голосовые связки, а врачи рекомендовали Джеку не петь и не говорить в течение двух недель.

Халберт напряг свою исполнительную мускулатуру, исключив обе франшизы из Лиги.

Вебер сказал, что фильм разрушил священные модальные округлости, напряг отношения в группе и сделал невозможным любое будущее воссоединение.

Вебер сказал, что фильм разрушил священные модальные округлости, напряг отношения в группе и сделал невозможным любое будущее воссоединение.

Другие результаты

Не в напряг как пишется

См. также напрячь .

Содержание

• 1.1.1 Морфологические и синтаксические свойства
• 1.1.2 Произношение
• 1.1.3 Семантические свойства

• 1.1.3.1 Значение
• 1.1.3.2 Синонимы
• 1.1.3.3 Антонимы
• 1.1.3.4 Гиперонимы
• 1.1.3.5 Гипонимы

1.1.4 Родственные слова

1.1.5 Этимология

1.1.6 Фразеологизмы и устойчивые сочетания

1. 1.7 Перевод

1.1.8 Библиография

1.2 напряг II

напряг I Править

В Викиданных есть лексема напряг (L131250).

Морфологические и синтаксические свойства Править

падеж	ед. ч.	мн. ч.
Им.	напря́г	напря́ги
Р.	напря́га	напря́гов
Д.	напря́гу	напря́гам
В.	напря́г	напря́ги
Тв.	напря́гом	напря́гами
Пр.	напря́ге	напря́гах

Корень: -напряг-; суффикс: -∅.

Произношение Править

• МФА: ед. ч. [ nɐˈprʲak ], мн. ч. [ nɐˈprʲæɡʲɪ ]

Семантические свойства Править

Значение Править

1. разг. — сниж.усилие, сильное напряжение или волнение ◆ Гостья моя, за которую я и глотка не отпил, сидит в напряге . А. Мамедов, И. Милькин, «Самому себе», 2002 г. // «Октябрь» ◆ Упирается ногой, тянет. Стонет от напряга . Едва повернув петли, протискивается внутрь. А. Иличевский, «Гладь», 2006 г. // «Новый Мир» ◆ Поэтому людям хочется всего и сразу, без какого-либо напряга … «Хватит губить детей!», 2011 г. (цитата из Национального корпуса русского языка, см. Список литературы)
2. разг. — сниж. затруднительное положение, неприятность ◆ Кстати, с дочкой напрягов поменьше было. «Наши дети: Подростки», 2004 г. (цитата из Национального корпуса русского языка, см. Список литературы)
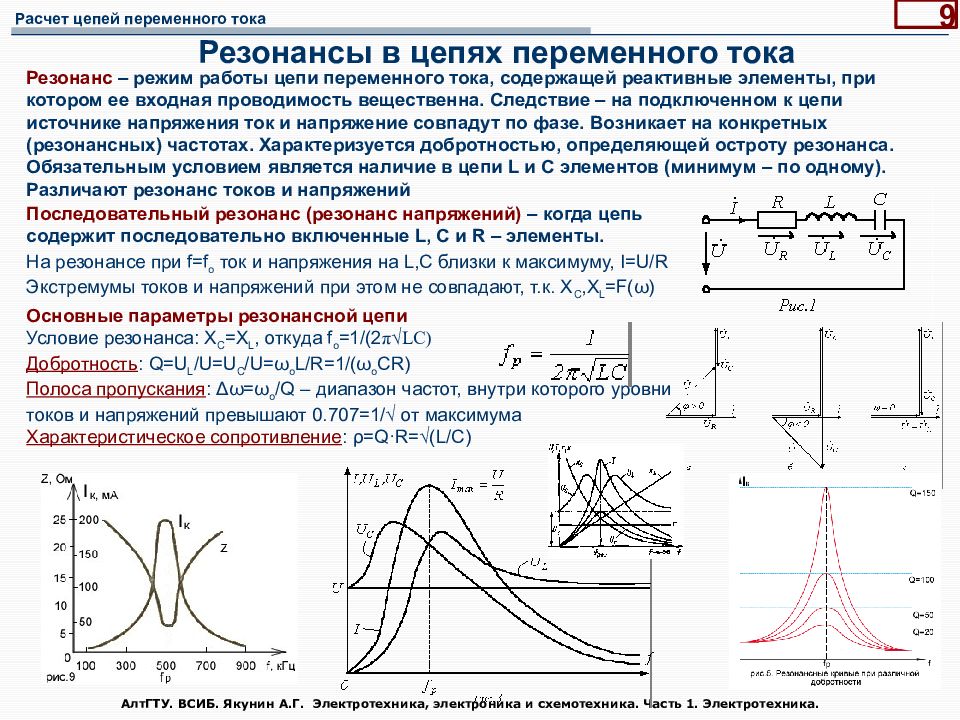
3. разг. — сниж.предик.отсутствие, нехватка чего-либо ◆ У мну со временем напряг конкретный для этого дела ◆ У меня есть в избытке первого и третьего, а вот со вторым — конкретный напряг , как оказалось

Синонимы Править

1. усилие
2. неприятность
3. отсутствие, нехватка

Антонимы Править

1. расслабленность
2. норма, будни
3. достаток

Гиперонимы Править

1. состояние
2. ситуация
3. ?

Гипонимы Править

1. —
2. —
3. —

Родственные слова Править

Этимология Править

Фразеологизмы и устойчивые сочетания Править

• быть в напряге

Перевод Править

• Английский en: trouble

Библиография Править

напряг II Править

• форма прошедшего времени мужского рода единственного числа изъявительного наклонения глагола напрячь

Автор: Анна Рожкова

Ударение.

Тип ударения. Место ударения.

Ударение

– это выделение одного слога из такта. Слог выделяется релятивной разницей в супрасегментных признаках между отдельными слогами такта.

По способу выделения слога из такта можно ударение подразделить на:

1. динамическое (экспираторное, силовое) – слог выделяется силой выдоха

2. квантитативное (количественное) – слог выделяется долготой

3. мелодическое (музыкальное, тоновое) – слог выделяется движением голосового тона.

Чистых типов ударения фактически не бывает, почти всегда один тип сопровождается другим, хотя один из них преобладает.

Динамическое ударение имеется в русском, английском, чешском и других языках. В русском языке динамическое ударение сопряжено с квантитативным.

Мелодическое ударение встречается, напр., в сербохорватском, литовском, китайском и др. яз.

Динамическое ударение бывает или сильное (в русском, английском и др. яз) или слабое (в чешском, грузинском и др.)

В языках с сильным динамическим ударением почти вся сила, выталкиваемой из лёгких струи воздуха, используется для произношения ударного слога. Для безударных слогов не достает силы, они ослабляются и изменяются.

Изменение звучания безударных слогов (прежде всего их сонорного центра) называется редукцией.

По способу выделения слога из такта в русском языке сильное динамическое ударение: гласные в безударных слогах редуцируются, что приводит к многообразию гласных звуков (аллофонов), в которых реализуется ограниченное количество фонем русского языка. Силе русского ударения сопутствует длительность – подударный слог русского слова не только самый сильный, а также самый долгий.

В чешском языке слабое динамическое ударение: гласные в безударных слогах почти не меняются.

Например:   zá-mek        ve-čer                 вé-чер       зá— мок       за – мóк

Длительность гласных звуков ЧЯ выполняет смысло-различительную функцию и не связана с динамичностью ударения. (т.е. она является свойством сегментных элементов) и не зависит от ударной или безударной позиции.Долгие гласные вдвое длительнее кратких.

Длительность гласных звуков РЯ не является самостоятельным свойством сегментных элементов, она сопутствует силе динамического ударения и является его второстепенной характеристикой. Подударные гласные в 2-3 раза дольше безударных.

Итак, в РЯ сильное динамическое ударение со значительным квантитативным компонентом.

В ЧЯ слабое динамическое ударение без квантитативного компонента.

Например:

ра –бó-тать         мо-ло-кó       о-го-рóд           rá-na       ra-ná     pra-co-vat     pa-má-tka

Место удаарения

По месту выделяемого слога в слове различаются:

1. фиксированное ударение (бывает всегда на определенном слоге – в ЧЯ на первом, во французском на последнем)

2. свободное (разноместное), которое не связано с определенным местом в слове, оно падает на любой слог, напр. , в РЯ, в английском. яз.

Свободное ударение имеет два подтипа:

1. свободное постоянное т.е. в разных формах данного слова ударение падает    всегда на тот же слог (в английском яз., в большинстве слов РЯ)

2. свободное подвижное т.е. в разных формах данного слова ударение падает на разные слоги (напр., в некоторых русских словах – мó-ре – мо-ря, пи-шу – пи-шешь).

В РЯ ударение свободное, подвижное и имеет функцию смысло-различительного, фонологического средства: зá-мок – за- мóк, пи-ли – пи-ли . В ЧЯ ударение фиксированное и не может приобрести фонологическую функцию.

Но подвижность русского ударения ограничена, в большинстве русских слов ударение постоянное.

Каждое самостоятельное слово РЯ имеет, как правило, одно ударение. Служебные и в немногих случаях также и некоторые самостоятельные слова не имеют на себе ударения и примыкают к соседнему слову как проклитики или энклитики.

Энклитиками являются некоторяе частицы, напр.: скажи-ка, учитель же сказал …, иногда это могут быть и самостоятельные слова, напр.: нé дал, нé жили, взять зá волосы и др.

Проклитиками обычно являются односложные предлоги, союзы, частицы и прочее, напр.: на завóде, об этом, не говорите…. Некоторые односложные предлоги в сочетании с определенными существительными иногда перетягивают ударение на себя (следующее слово становится безударным, энклитическим). Напр.: нá голову, зá руку, пóд руку, бéз вести …(в ЧЯ это касается почти всех предлогов).

Двухсложные и трехсложные служебные слова бывают или безударными или слабоударяемыми (с побочным ударением), напр., через чáс или чéрез чáс.

Многосложные словa, образованные путем сложения двух или больше основ, имеют наряду с основным ударением еще одно (или больше) — побочное. Основное ударение падает всегда на ударный слог последней основы многосложного слова, побочные бывают ближе к его началу, напр., дáльневостóчный, рáдиопередáча. Сложные слова, небольшие по объему, побочного ударения не имеют: паровóз, садовóд.

Упражнение 4.1

Читайте, следите за изменением ударения в родственных словах

Гóрод – городá – гóрода – огорóд – городовóй – зáгородного

Хóлод – холодá – хóлодно – холодновáто – похолодáло

Гóлос – голосá – гóлоса – голосовóй – подголóсок

Морóз – зáморозки – подморозило – выморозило – морóзного

Ворóт – ворóта – подворóтня – воротничóк – подворотничóк

Бородá – бóроды – подборóдок – бородáвка

Рабóта – зарабóток – зарабóтал – выработал

Зóлото – золотистый – позолóта – позолóченный

Вóрон – ворóна – воронóй – вороньё – воронёнок

Упражнение 4.

2

Образуйте слова по образцу, следите за ударением

Образец: подарить – подáрок

Отрывáть —		поступáть —		снимáть —
Слепить —		набросáть —		обломáть
Обрезáть —		недовéсить —

Упражнение 4.

3

Образуйте слова данной ритмической модели

тá –та

та – тá

та – та – тá

та – тá – та

тá – та – та

Упражнение 4.4

Расставьте ударение

Город, доктор, доклад, завод, фотограф, пароход, композитор, альбом, овраг, аппарат, овощи, комната, автомашина, собака, дорога, скала, голова, борода, оса, окно, остановка, куколка, бабушка, отец, сестра, лекарство, отчество, берег, без места, под окном, в лесу, на столе, под снегом, у дома, у города, над дверью, по полю, через реку.

Упражнение 4.5

Читайте, следите за ударением и правильным произношением

Век – векá, тело – телá, дело – делá, лес – лесá, цвет – цветá

Пять – пяти, взял – взялá, снял – снялá, тянут – тяни.

Урок был подготовлен с использованием следующей литературы:

Теоретическая часть

[1]Оливериус, З. Фонетика русского языка. Praha : SPN, 1978. 164 c.

[2]Брызгунова, Е. А. Звуки и интонации русской речи. Москва : Русский язык, 1977. 279 с.

Практическая часть

[1]Бархударова, Е. Л. – Панков, Ф. И. По-русски с хорошим произношением. Практический курс звучащей речи. Москва : Русский язык, 2008. 192 с. ISBN 978- 5-88337-160-7.

[2]Одинцова, И. В. Звуки. Ритмика. Интонация. Москва : Наука, 2008. 368 с. ISBN 978- 5-02-002762-6.

[3]Лизалова, Л. И. Упражнения по фонетике современного русского языка. Брно : МУ, 1991. 78 с.

Напряжение — AP Physics 1

Пояснение:

Чтобы найти массу блока 2, нам нужно будет вычислить еще несколько вещей, например, натяжение веревки.

Для начала нам нужно определить различные силы на нашей диаграмме свободного тела. Для этого мы начнем с блока 1 и будем использовать повернутую систему координат для упрощения. В такой системе ось X будет проходить параллельно поверхности пандуса, а ось Y будет перпендикулярна поверхности пандуса, как показано ниже:

Теперь мы можем определить силы, действующие на блок 1.Вдоль повернутой оси Y сила тяжести, действующая на блок, равна, а сила наклонной поверхности на блоке равна нормальной силе,. Поскольку блок 1 не движется в направлении y, мы можем установить эти две силы равными друг другу.

Теперь, учитывая силы, действующие вдоль повернутой оси x, мы имеем силу, направленную вниз, равную. Если направить вверх, у нас есть сила натяжения и сила трения.

Формула для расчета силы кинетического трения:

Поскольку мы уже определили, что такое нормальная сила, мы можем подставить это выражение в приведенное выше уравнение, чтобы получить:

Теперь мы можем написать выражение для чистой силы, действующей на блок 1 в направлении x:

Измените приведенное выше выражение, чтобы найти натяжение.

До сих пор мы рассматривали только блок 1. Теперь давайте обратим наше внимание на блок 2 и посмотрим, какие силы действуют на него. В направлении вниз у нас есть вес блока из-за силы тяжести, который равен. В восходящем направлении, как мы видим на диаграмме, натяжение веревки. Нам нужно написать выражение, которое сообщает нам чистую силу, действующую на блок 2.

Поскольку мы вычислили выражение для натяжения на основе информации о блоке 1, мы можем вставить это выражение в приведенное выше уравнение, чтобы получить:

Теперь переставьте, чтобы вычислить массу блока 2.

Затем, подставив значения, мы можем, наконец, вычислить массу блока 2:

Нормальные, растягивающие и другие примеры сил

Пример 1. Вес на уклоне, двумерная задача

Рассмотрим лыжника на склоне, показанном на рисунке 2. Ее масса, включая снаряжение, составляет 60,0 кг. а) Каково ее ускорение, если трение незначительно? (б) Каково ее ускорение, если известно, что трение равно 45.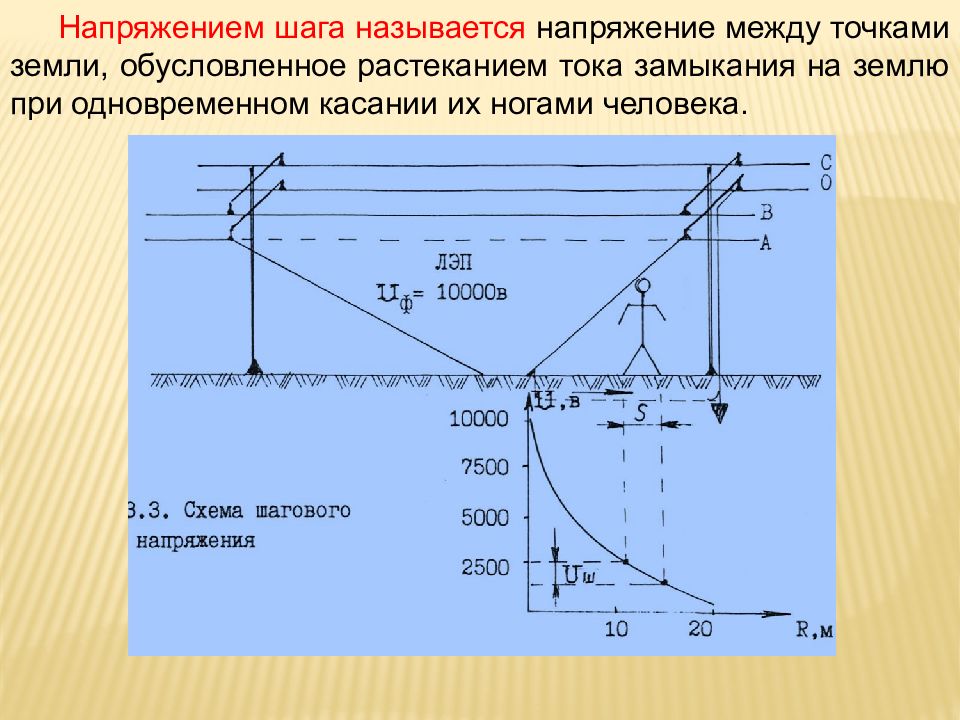 0 N?

Рис. 2. Поскольку движение и трение параллельны склону, наиболее удобно проецировать все силы в систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). N перпендикулярно откосу, а f параллельно склону, но w имеет компоненты вдоль обеих осей, а именно w _⊥ и [латекс] \ textbf {w} _ {\ parallel} [ /латекс]. N равно по величине w _⊥ , так что нет движения, перпендикулярного уклону, но f меньше w∥, так что есть ускорение вниз по склону (вдоль параллельной оси).

Стратегия

Это двумерная задача, поскольку силы, действующие на лыжника (интересующая система), не параллельны. Подход, который мы использовали в двумерной кинематике, также здесь очень хорошо работает. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав , две , связанные, , одну -мерную задачу, которую нужно решить.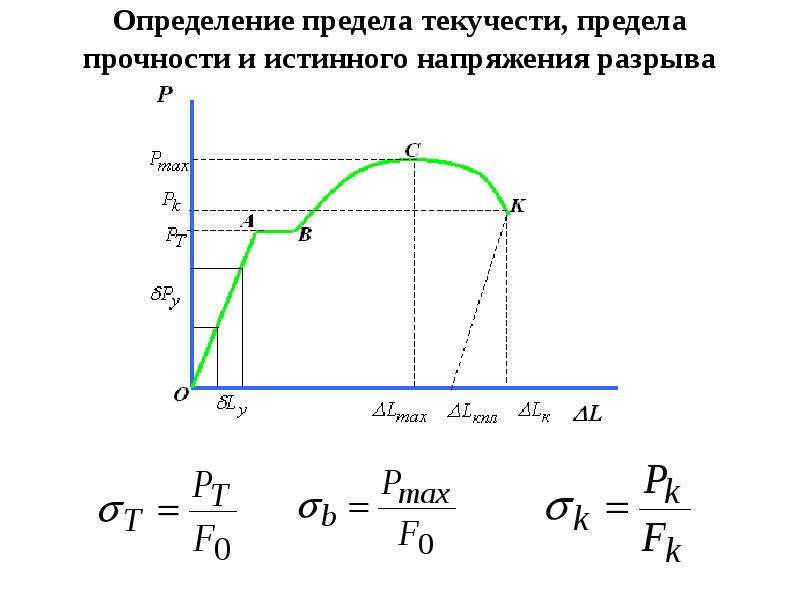 Самая удобная система координат для движения по наклонной поверхности — это та, в которой одна координата параллельна склону, а другая — перпендикулярна склону.(Помните, что движения по взаимно перпендикулярным осям независимы.) Мы используем символы ⊥ и ∥ для обозначения перпендикуляра и параллельности соответственно. Такой выбор осей упрощает этот тип проблемы, потому что нет движения, перпендикулярного уклону, и потому что трение всегда параллельно поверхности между двумя объектами. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и поддержка склона, обозначенные соответственно w , f и N на Рисунке 2.N всегда перпендикулярно откосу, а f параллельно ему. Но w не находится в направлении ни одной из осей, и поэтому первый шаг, который мы делаем, — проецируем его на компоненты вдоль выбранных осей, определяя w _∥ как составляющую веса, параллельную наклону, и w _⊥ компонент веса, перпендикулярный уклону. 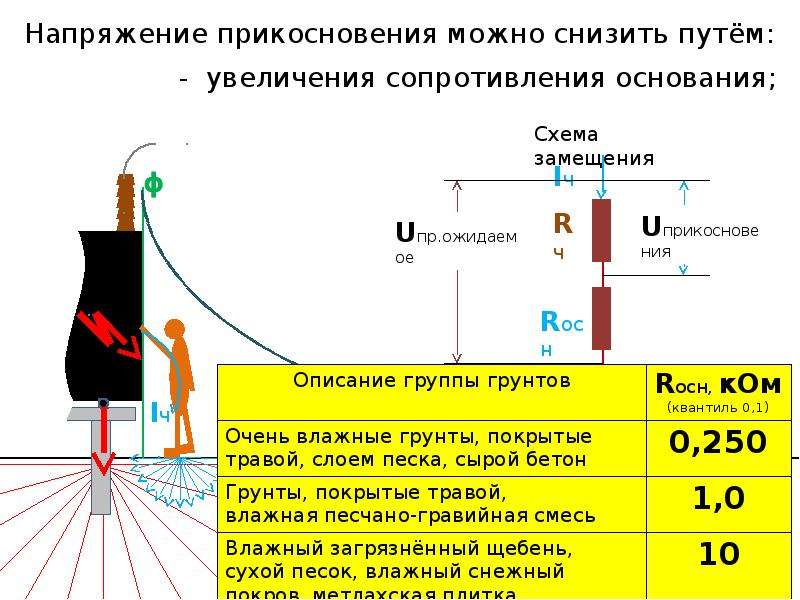{\ circ}) — f} {m} [/ latex].{2} [/ латекс]

, что соответствует ускорению, параллельному наклону, при противоположном трении 45,0 Н.

Обсуждение

Поскольку трение всегда противостоит движению между поверхностями, ускорение меньше при трении, чем при его отсутствии. Фактически, общий результат заключается в том, что если трение на уклоне незначительно, то ускорение вниз по уклону составляет a = g sin θ , независимо от массы .Это связано с ранее обсуждавшимся фактом, что все объекты падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).

Задачи двух тел

В блоке законов Ньютона введена тема задач двух тел. Была обсуждена пара стратегий решения проблем, которые были применены для решения трех примеров проблем. Такие проблемы с двумя телами обычно включают решение для ускорения объектов и силы, действующей между объектами.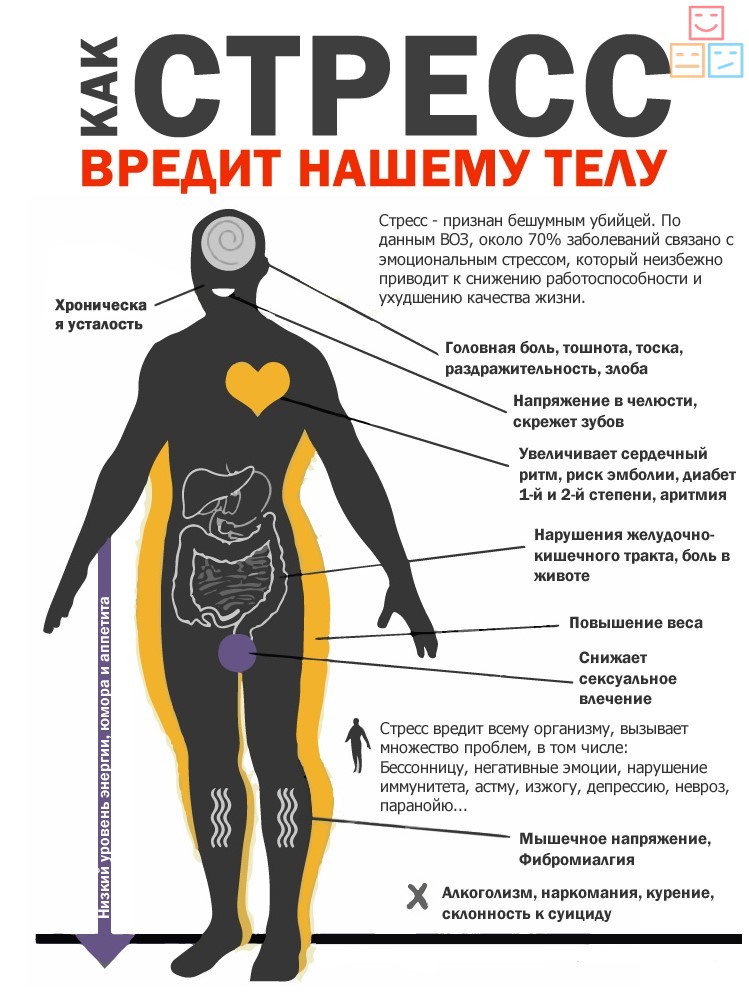 Одна из стратегий решения задач двух тел включает использование системного анализа для определения ускорения в сочетании с анализом отдельного объекта для определения силы, передаваемой между объектами. Вторая стратегия заключалась в использовании анализа двух отдельных объектов с целью разработки системы из двух уравнений для решения двух неизвестных величин. При необходимости найдите время, чтобы просмотреть страницу о решении задач двух тел. Эта страница будет основываться на уроках, извлеченных ранее в разделе «Законы Ньютона».

В этом уроке мы проанализируем задачи о двух телах, в которых объекты движутся в разных направлениях. В этих задачах два объекта связаны цепочкой, которая передает силу одного объекта другому. Струна наматывается на шкив, который изменяет направление приложения силы без изменения величины. В качестве иллюстрации того, как работает шкив, рассмотрим схему справа. Объект A связан с объектом B строкой. Веревка наматывается на шкив в конце стола.Объект A подвешен в воздухе, а объект B лежит на столе. В этой ситуации объект А упадет вниз под действием силы тяжести, потянув вниз один конец струны, к которой он подсоединен. Согласно закону действия-противодействия Ньютона, этот нижний конец струны будет тянуть вверх на объект A. Противоположный конец струны соединен с объектом B. Этот конец струны тянет вправо на объект B. соединение двух объектов притягивает оба объекта с одинаковой силой, но в разных направлениях.Трос тянет вверх на объект A и вправо на объект B. Шкив изменил направление приложения силы.

Проблемы, связанные с двумя объектами, соединительными цепями и шкивами, характеризуются объектами, которые движутся (или даже ускоряются) в разных направлениях. Они движутся или ускоряются с одинаковой скоростью, но в разных направлениях. Таким образом, при решении таких задач становится важным выбрать другую систему отсчета и систему осей для каждого объекта.Следует обратить внимание на такой выбор системы осей, чтобы оба объекта ускорялись вдоль оси в положительном направлении. С осями, правильно определенными для каждого отдельного объекта, можно построить диаграмму свободного тела. Затем к каждой диаграмме можно применить законы Ньютона, чтобы получить систему из двух уравнений для решения двух неизвестных. Этот процесс решения проблем будет продемонстрирован на трех различных примерах задач.

Пример задачи 1

А 200.Масса 0 грамм (m ₁ ) и масса 50,0 грамм (m ₂ ) соединены веревкой. Струна натянута на шкив. Определите ускорение масс и натяжение струны.

Как это часто бывает, в этом примере проблема запрашивает информацию о двух неизвестных — ускорении объектов и силе, действующей между объектами. В такой ситуации, как эта, когда два объекта подвешены на шкиве, более массивный объект будет ускоряться вниз, а наименее массивный объект будет ускоряться вверх.Величина ускорения будет одинаковой для каждого объекта. Система координат, выбранная для m ₁ , имеет положительную ось y, направленную вниз; система координат, выбранная для m ₂ , имеет положительную ось y, направленную вверх. При таком выборе осей направление ускорения будет положительным для каждого объекта. Диаграммы свободного тела для каждой индивидуальной массы показаны ниже. Каждый объект испытывает нисходящую силу тяжести, которая рассчитывается как ₁ • g и ₂ • g м соответственно.Каждый объект также испытывает восходящую силу натяжения, которая притягивает два объекта друг к другу.

Уравнение второго закона Ньютона (F _net = m • a) можно применить к обеим диаграммам, чтобы написать два уравнения для двух неизвестных. F _net будет выражаться как сила в направлении ускорения минус сила, которая ему противодействует. Таким образом, для массы 200,0 грамм F _net записывается как 1,960 N — F _{десятки} .Для массы 50,0 грамм F _net записывается как F _{десятки} — 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 и 50,0 граммов. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)

1,960 — F _{десятки} = 0,2000 • a

Ж _{десятки} — 0.490 = 0,0500 •

С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 2 можно переформулировать, чтобы получить выражение для F _{десятков} , записанное в терминах ускорения.

F _{десятки} = 0,0500 • a + 0,490

Это выражение для F _{десятков} теперь можно подставить в уравнение 1, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.

1,96 — (0,0500 • a + 0,490) = 0,2000 • a
1,96 — 0,0500 • а — 0,490 = 0,2000 • а
1,47 = 0,2500 •
a = 1,47 / 0,2500 = 5,88 м / с ²

Теперь, когда ускорение было найдено из уравнения 1, его значение можно подставить в уравнение 3, чтобы определить натяжение.

F _{десятки} = 0,0500 • (5,88) + 0,490
F _{десятки} = 0,784 N

Проанализированную здесь систему шкивов иногда называют машиной Атвуда.Подход к решению проблем — это стандартный подход, который будет использоваться на этой странице для решения двух неизвестных. Он будет повторен в примере проблемы 2, чтобы решить то, что обычно называют модифицированной машинной проблемой Этвуда.

Пример задачи 2

Рассмотрим ситуацию с двумя телами справа. К подвеске 250 крепится 20-граммовый подвесной груз (m ₂ ).0-граммовый гусеничный планер ( _{м 1} ). Определите ускорение системы и натяжение струны.

Как и в примере проблемы 1, эта система должна быть сначала проанализирована концептуально, чтобы определить направление ускорения двух объектов. Это позволит назначить оси координат для каждого объекта. Поскольку ничто не толкает m ₁ влево, мы можем предположить, что он будет ускоряться вправо из-за натяжения струны.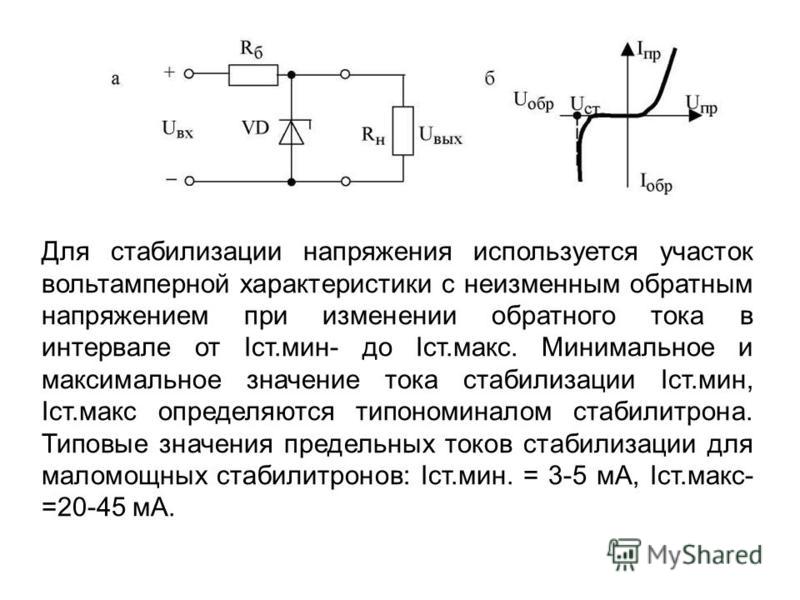 Висящая масса (m ₂ ) будет явно ускоряться вниз под действием силы тяжести. Таким образом, система координат выбрана для m ₂ имеет положительную ось y, направленную вниз; система координат, выбранная для m ₁ , имеет положительную ось x, направленную вправо. При таком выборе осей направление ускорения будет положительным для каждого объекта.

Диаграмма свободного тела для каждой отдельной массы показана ниже. Каждый объект испытывает нисходящую силу тяжести (F _grav ), рассчитываемую как ₁ • g и ₂ • g м соответственно.Планер (m ₁ ) испытывает восходящую опорную силу (воздух толкает его вверх), чтобы уравновесить силу тяжести. Планер также испытывает горизонтальную силу — силу натяжения (F _{десятки} ) вправо. Висящая масса (m ₂ ) испытывает восходящую силу натяжения (F _{десятки} ), которая оказывает некоторое сопротивление нисходящему притяжению силы тяжести.

Уравнение второго закона Ньютона (F _net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.F _net будет выражаться как сила в направлении ускорения минус все, что ему противодействует. Для параплана массой 250,0 грамм (0,250 кг) F _net — это просто неуравновешенная сила натяжения (F _{десятки} ). Для подвешенной массы 20,0 грамм (0,020 кг) F _net записывается как 0,196 N — F _{десятки} . Уравнения 4 и 5 являются результатом применения уравнения второго закона Ньютона к 250,0-граммовому планеру и 20,0-граммовой висящей массе. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях.Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)

F _{десятки} = 0,2500 • a

0,196 — F _{десятки} = 0,0200 • a

С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 4 выражает значение F _{десятков} с точки зрения ускорения. Это выражение для F _{десятков} можно подставить в уравнение 5, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.

0,196 — 0,2500 • a = 0,0200 • a
0,196 = 0,2700 •
a = 0,196 / 0,2700 = 0,72593 м / с ²
а = ~ 0,726 м / с ²

Теперь, когда ускорение было найдено из уравнения 5, его значение можно подставить в уравнение 4, чтобы определить натяжение.

F _{десятки} = 0,2500 • (0.72593) = 0,18148
F _{десятков} = ~ 0,181 Н

Система шкивов, проанализированная в примере задачи 2, иногда называется модифицированной машиной Атвуда. Анализ немного сложнее, чем машина Атвуда в примере задачи 1. Последний пример задачи будет представлять собой случай модифицированной машины Атвуда с поверхностью, наклоненной, как показано ниже. Подход к решению проблем будет таким же.

Пример задачи 3

Рассмотрим ситуацию с двумя телами справа.Ящик 2,50×10 ³ кг (m ₁ ) стоит на наклонной плоскости и соединяется кабелем с массой 4,00×10 ³ кг (m ₂ ). Эта вторая масса ( ₂ m) подвешена на шкиве. Угол наклона 30,0 °, поверхность не имеет трения. Определите ускорение системы и натяжение троса.

Как и предыдущая задача, первая задача включает анализ ситуации, чтобы определить, в каком направлении объекты будут ускоряться.Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса ( ₂ m) могла ускоряться вверх или вниз. Направление его ускорения зависит от сравнения его веса (силы тяжести) с противоположной силой, действующей на другую массу (m ₁ ). Масса на наклонной плоскости сталкивается с тремя силами — силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена ​​вниз (как обычно) и рассчитывается как m ₁ • g.Нормальная сила направлена ​​перпендикулярно поверхности (как обычно). Сила натяжения направлена ​​вверх и вправо — параллельно наклонной плоскости и в той же ориентации, что и струна, обеспечивающая эту силу. Как обсуждалось на предыдущей странице, объекты, размещенные на наклонных плоскостях, анализируются путем разделения силы тяжести на две составляющие. Один компонент направлен параллельно плоскости (и вниз под этим углом), а другой компонент направлен перпендикулярно плоскости (и вверх под этим углом).Это параллельная составляющая силы тяжести, которая пытается увести m ₁ вниз по наклонной плоскости. Как упоминалось ранее, этот компонент может быть вычислен путем умножения веса объекта (m ₁ • g) на синус угла наклона (30 °). Значение для F _parallel равно

.

F _{параллельно} = м ₁ • g • синус (θ) = (2500 кг) • (9,8 Н / кг) • синус (30 °)
F _{параллельно} = 12250 Н

Этот параллельный компонент силы тяжести пытается увести m ₁ вниз по наклонной плоскости. Поскольку m ₁ прикреплен тросом к m ₂ , подвешенная масса будет тянуться вместе с ним. Однако есть противоположное действие силы тяжести, тянущее вниз m ₂ ; это противоположное действие, если оно будет преобладающим, перетащит объект m ₁ вверх по наклонной плоскости. Сила тяжести на ₂ м составляет

F _grav-2 = m ₂ • g = (4000 кг) • (9,8 Н / кг) = 39200 Н

Эта гравитационная сила на м. ₂ является доминирующей силой.Таким образом, m ₁ будет ускоряться вверх по наклонной плоскости, а m ₂ будет ускоряться вниз. Оси координат назначаются соответственно так, чтобы каждый объект имел положительное ускорение.

На схемах ниже показаны эти оси координат и силы, действующие на два объекта. Три силы на m ₁ уже обсуждались. На схеме показаны два компонента F _grav . Как упоминалось на предыдущей странице, перпендикулярная составляющая силы тяжести рассчитывается как

.

F _{перпендикуляр} = m ₁ • g • cosθ = (2500 кг) • (9.8 Н / кг) • cos (30 °)
F _{перпендикуляр} = 21218 Н

Нормальная сила (F _норма ), действующая на m ₁ , уравновешивает F _{перпендикуляр} , так что нет ускорения, перпендикулярного наклонной плоскости. Значение нормы F _{также составляет 21218 Н. Висящая масса (m 2 ) испытывает только две силы — силу тяжести, направленную вниз, и силу натяжения вверх.}

Теперь уравнение второго закона Ньютона (F _net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.F _net выражается как сила в направлении ускорения за вычетом любой силы, которая ему противодействует. Для груза массой 2500 кг на уклоне ( _{м 1} ), F _net — это просто сила натяжения (F _{десятки} ) за вычетом параллельной составляющей силы тяжести. Для подвешенной массы 4000 кг ( ₂ м) F _net представляет собой силу тяжести (39200 Н) за вычетом силы натяжения (F _{десятки} ). Уравнения 6 и 7 являются результатом применения уравнения второго закона Ньютона к m ₁ и m ₂ .(Обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)

F _{десятки} — 12250 = 2500 •

39200 — F _{десятки} = 4000 • a

С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 6 можно переформулировать, чтобы получить выражение для F _{десятков} , выраженное в единицах ускорения.

F _{десятки} = 2500 • a + 12250

Это выражение для F _tens можно подставить в уравнение 7, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.

39200 — (2500 • a + 12250) = 4000 • a
39200 — 2500 • a — 12250 = 4000 • a
26950 = 6500 •
a = 26950/6500 = 4,1462 м / с ²
а = ~ 4,15 м / с ²

Теперь, когда ускорение было найдено из уравнения 7, его значение можно подставить в уравнение 8, чтобы определить силу натяжения (F _{десятки} ).

F _{десятки} = 2500 • a + 12250 = 2500 • (4,1462) + 12250 = 22615 N
F _{десятки} = ~ 2,26 x 10 ⁴ N

Задачи с двумя телами, подобные этим трем примерам задач, могут быть довольно сложной задачей. Системный подход, применяемый к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона — вот основные составляющие успеха.

Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора машины Этвуда. Вы можете найти его в разделе Physics Interactives на нашем сайте. Тренажер позволяет исследовать двухмассовые системы, ускоряемые подвешенной массой.

Проверьте свое понимание

1. Рассмотрим ситуацию с двумя телами справа. 100,0-граммовая подвешенная масса (m2) прикрепляется к 325,0-граммовой массе (m1), покоящейся на столе. Коэффициент трения между 325,0-граммовой массой и столом составляет 0,215. Определите ускорение системы и натяжение струны.

2. Рассмотрим ситуацию с двумя телами справа.Ящик 3,50×10 ³ кг (m ₁ ) стоит на наклонной плоскости и соединяется кабелем с массой 1,00×10 ³ кг (m ₂ ). Эта вторая масса ( ₂ m) подвешена на шкиве. Угол наклона составляет 30,0 °, а поверхность имеет коэффициент трения 0,210. Определите ускорение системы и натяжение троса.

Лаборатория 3 — Второй закон Ньютона

Введение

Сэр Исаак Ньютон выдвинул много важных идей в своей знаменитой книге The Principia .Его три закона движения — самые известные из них. Кажется, что первый закон противоречит нашему повседневному опыту. Первый закон Ньютона гласит, что любой объект в состоянии покоя, на который не действуют внешние силы, будет оставаться в состоянии покоя, и что любой объект в движении, на который не действуют внешние силы, будет продолжать движение по прямой линии с постоянной скоростью. Если мы катим мяч по полу, мы знаем, что он в конечном итоге остановится, что, по-видимому, противоречит Первому закону. Наш опыт, кажется, согласуется с идеей Аристотеля о том, что «импульс», придаваемый мячу, исчерпывается по мере его катания.Но Аристотель ошибался, как и наше первое впечатление о движении мяча. Суть в том, что мяч действительно испытывает внешнюю силу, то есть трение, на мяч , когда он катится по полу. Эта сила заставляет мяч замедляться (то есть имеет «отрицательное» ускорение). Согласно второму закону Ньютона объект будет ускоряться в направлении чистой силы . Поскольку сила трения противоположна направлению движения, это ускорение заставляет объект замедлять свое поступательное движение и в конечном итоге останавливаться.Цель этого лабораторного упражнения — проверить второй закон Ньютона.

Обсуждение принципов

Второй закон Ньютона в векторной форме имеет вид Эта сила заставляет шарик, катящийся по полу, замедляться (то есть иметь «отрицательное» ускорение). Согласно второму закону Ньютона, объект будет ускоряться в направлении действующей силы. Если

F

— это величина чистой силы, и если

м

— это масса объекта, то ускорение определяется по формуле

(2)

а =

F

м

Поскольку сила трения имеет направление, противоположное направлению движения, это ускорение заставляет объект замедлять свое поступательное движение и в конечном итоге останавливаться.Обратите внимание, что уравнение. (1) и уравнение. (2) a =

F

m

записываются в векторной форме. Это означает, что второй закон Ньютона верен во всех направлениях. Вы всегда можете разделить силы и результирующее ускорение на соответствующие составляющие в направлениях

x

,

y

и

z

. Рассмотрим тележку на гусенице с низким коэффициентом трения, как показано на рис. 1. Легкая струна прикреплена к тележке и проходит через шкив в конце гусеницы, а к концу этой струны прикреплена вторая масса.Вес подвешенной массы обеспечивает натяжение тетивы, что способствует ускорению тележки по рельсам. Этому движению будет сопротивляться небольшая сила трения. Мы предполагаем, что струна не имеет массы (или имеет незначительную массу) и что между струной и шкивом нет трения. Следовательно, натяжение струны будет одинаковым во всех точках струны. Это приводит к тому, что обе массы имеют одинаковую величину ускорения, но направление ускорения будет разным. Тележка будет ускоряться вправо, в то время как висящая масса будет ускоряться в направлении вниз, как показано на рис.1.

Рисунок 1 : Двухмассовая система

Мы возьмем положительное направление в направлении ускорения двух масс, как показано системой координатных осей на рис. 1. Диаграммы свободного тела для двух масс показаны на рис. 2. Давайте посмотрим на силы. действуя на каждую массу.

Рисунок 2 : Диаграммы свободного тела для двух масс

Для падающей массы

м ₁

отсутствуют силы, действующие в горизонтальном направлении.В вертикальном направлении он тянется вниз под действием силы тяжести, придавая объекту вес

W = m ₁ г

, и вверх за счет натяжения

T

в струне. См. Рис. 2b. Таким образом, второй закон Ньютона, примененный к падающей массе в направлении

y

, будет выглядеть так:

(6)

F _{net, 1} = m ₁ g — T = m ₁ a

где направление вниз было выбрано положительным.На рис. 2а показаны силы, действующие на

м ₂

. Тележка в вертикальном направлении не движется. Следовательно, чистая сила в вертикальном направлении будет равна нулю, как и ускорение. В горизонтальном направлении натяжение струны действует на тележку в направлении

+ x

, в то время как сила трения между шинами тележки и поверхностью гусеницы действует в направлении

— x

. Второй закон Ньютона в направлениях

x

и

y

соответственно равен

(7)

F _{net, 2x} = T — f = m ₂ a

(8)

F _{net, 2y} = F _N — m ₂ g = 0

Поскольку тележка и подвешенный груз связаны веревкой, которая не растягивается, оба ускорения, появляющиеся в уравнении.(6)

F _{net, 1} = m ₁ g — T = m ₁ a

и уравнение. (7)

F _{net, 2x} = T — f = m ₂ a

представляют те же физические свойства. Напряженность такая же из-за третьего закона Ньютона. Объедините уравнение. (6)

F _{net, 1} = m ₁ g — T = m ₁ a

и уравнение. (7)

F _{net, 2x} = T — f = m ₂ a

для исключения

T

.

(9)

м ₁ г = (м ₁ + м ₂ ) a + f

Обратите внимание, что уравнение.(9)

m ₁ g = (m ₁ + m ₂ ) a + f

имеет форму линейного уравнения

y = mx + b

, где m — наклон, а

b

— это перехват

и

.

Цель

Цель этого эксперимента — проверить справедливость второго закона Ньютона, который гласит, что результирующая сила, действующая на объект, прямо пропорциональна его ускорению. Уравнение (9)

m ₁ g = (m ₁ + m ₂ ) a + f

было получено на основании этого закона.Поэтому мы можем рассмотреть уравнение. (9) быть предсказанием второго закона. В этом эксперименте мы постараемся проверить это конкретное предсказание и тем самым предоставить доказательства справедливости второго закона.

Оборудование

• Гусеница с низким коэффициентом трения со шкивом
• Корзина
• Нить
• Баланс
• Программное обеспечение DataStudio
• Два фотоката
• Ассорти масс
• Весовая вешалка
• Компьютер
• Сигнальный интерфейс

Процедура

Вы проведете несколько испытаний, сохраняя общую массу

M = m ₁ + m ₂

постоянной при изменении

m ₁

и, следовательно,

m ₂

, чтобы получить другое значение

a

для каждого значения

м ₁

.Построив график

,

и

м ₁ г

, вы сможете найти

M

, общую массу системы из уравнения. (9)

m ₁ g = (m ₁ + m ₂ ) a + f

. К тележке прикреплен металлический флажок, который заставит два фотозатвора, размещенных на фиксированном расстоянии друг от друга, реагировать, когда тележка проходит через них. Компьютер, подключенный к фотозатвору, будет измерять и отображать временные интервалы, прошедшие, пока флаг проходит через два фотозабора.По этим временным интервалам и длине флага компьютер вычислит скорости

v ₁

и

v ₂

тележки на каждом из фотозатворов. Кроме того, из компьютерных данных вы можете определить интервал времени

Δt

, который требуется тележке для перемещения между фотозатвором. Тогда ускорение

a

между двумя воротами можно рассчитать по формуле где

v ₁

— скорость на первом фотозатворе, а

v ₂

— скорость на втором фотозатворе.

Настройка оборудования

1

Используя регулировочные винты под ними, выровняйте гусеницу так, чтобы тележка не двигалась, когда она размещается в центре гусеницы. Поскольку тележка имеет некоторое трение, проверьте, выровнена ли гусеница, слегка подтолкнув тележку вправо и сравнив движение с аналогичным толчком влево.

2

Разместите фотошиты достаточно далеко друг от друга. Убедитесь, что флажок тележки находится перед первыми воротами, когда подвеска полностью поднята рядом со шкивом, как показано на рис.3а. Кроме того, убедитесь, что флаг тележки проходит через второй фотозатвор до того, как вешалка упадет на землю. См. Рис. 3b. Это обеспечит ускорение тележки в области между двумя фотозатвором.

3

Отрегулируйте высоту каждой заслонки так, чтобы небольшой металлический флажок на тележке блокировал световой луч фотозатвора, когда он проходит.

Рисунок 3 : Установка фотозатвора

Рисунок 4 : Экспериментальная установка

4

Подключите фотозатвор 1 к цифровому каналу 1, а фотозатвор 2 — к цифровому каналу 2.Если фотозатворы подключены правильно, красный светодиод на фотозатворе загорится, когда инфракрасный луч заблокирован.

5

Откройте соответствующий файл Capstone, связанный с этой лабораторной работой. На рис. 5 показан начальный экран в Capstone.

Рисунок 5 : Отображение второго закона Ньютона

6

Длина небольшого металлического флажка на тележке разная для каждой тележки. Измерьте свою тележку и запишите это на листе.

7

Вы должны ввести значение длины флажка и расстояния между фотозатвором, как показано на рис. 6. Не забудьте нажать кнопку «Сохранить».

Рисунок 6 : Ввод длины флажка

Сбор данных

8

Поместите тележку в конце гусеницы подальше от шкива. Добавьте в корзину три гири по 50 грамм.

9

Взвесьте весовую подвеску и запишите на листе массу

M _h

.

10

Подсоедините один конец веревки к подвеске груза, а другой конец — к тележке, поместив веревку на шкив. См. Рис.3.

11

Удерживайте тележку в таком положении, чтобы при отпускании тележка ускорялась. Когда будете готовы к записи данных, нажмите кнопку Start . Освободите тележку и поймайте ее, когда она достигнет конца пути. Нажмите кнопку Stop , чтобы завершить запись данных. Данные о времени и скорости для каждого фотозатвора будут автоматически представлены в таблице.См. Рис.7.

Рисунок 7 : Пример таблицы данных

12

Скорость тележки плавно увеличивается в течение промежутка времени, пока флаг проходит через луч фотозатвора. В какой-то момент в течение этого интервала времени мгновенная скорость тележки равна средней скорости за интервал. Этот момент времени отображается в столбце «Время (с)» рядом с соответствующей скоростью.

13

Время, которое потребовалось для перемещения тележки между фотозатвором 1 и 2, составляет

Δt

.Это вычисляется путем вычитания значения времени в столбце Velocity in Gate, Ch2 из значения времени в столбце Velocity in Gate, Ch 2. Вычислите

Δt

и запишите это в Таблицу данных 1 на рабочем листе.

14

Используйте этот временной интервал вместе с двумя скоростями

v ₁

и

v ₂

в уравнении. (10), чтобы вычислить ускорение тележки между двумя фотозатвором и записать этот результат в Таблицу данных 1.

15

Переместите одну 50-граммовую гирю из тележки на вешалку. Примечание : Вы должны поддерживать постоянную общую массу, поэтому любую массу, снятую с тележки, необходимо добавить на грузоподъемник.

16

Повторите шаги с 11 по 15 еще три раза, пока у вас не будет в общей сложности четырех прогонов с разными значениями подвешенной массы для каждого прогона. Рассчитайте и запишите ускорение для каждого случая.

Контрольная точка 1:
Попросите своего технического специалиста проверить значения в таблице, прежде чем продолжить.

Анализ результатов

17

Используя график Excel

m ₁ g

по сравнению с

a

. См. Приложение G.

18

Используйте параметр линии тренда в Excel, чтобы нарисовать наиболее подходящую линию для данных и определить наклон и интервал

y

. См. Приложение H. Запишите эти значения на листе.

19

По величине уклона определяют общую массу системы.

20

Используйте весы, чтобы измерить массу тележки.Добавьте это к массе подвески груза и добавленным массам, чтобы получить общую массу

M

системы.

21

Сравните эту измеренную массу с массой, определенной по наклону графика, вычислив разницу в процентах. Запишите это на листе. См. Приложение Б.

Контрольная точка 2:
Попросите своего технического специалиста проверить ваш рабочий лист Excel и график.

Авторские права © 2012 Advanced Instructional Systems Inc.и государственный университет Северной Каролины | Кредиты

Boddeker 131 Ch 5 Домашнее задание

канат 5 шкив

Два объекта связаны легкой струной, проходящей через шкив без трения. (а) Нарисуйте диаграммы свободного тела обоих объекты. Если наклон без трения и если м 1 = 5,00 кг, м 2 = 10,00 кг и q = 60,0, найти (б) ускорения объектов, (в) натяжение в строке, и (d) скорость каждого объекта 2.00 с после выхода от отдыха.
(а) Схема свободного тела	(б) sin 60 = F в директории / 100 Н F 2 дюйма, реж. = 86,6 N F net = m T a F 2 дюйма, реж. м 1 г = м T a 86.6N 50N = (5 + 10) а а = 2,44 м / с 2		(в) Т 1 = м 1 (г + а) Т 1 = 5 (10 + 2.44) T 1 = 62,2 N Или жесткий способ!!! T 2 = m 2 (sin 60 g — а) T 2 = 10 (sin 60 10-2.44) T 2 = 62,2 N
			(г) а = Dv / Dt 2,44 = v f / 2 v f = 4,88 м / с

Ч 5 трение

Пуск блока 10,0 кг из состояния покоя на вершине уклона 30,0 и скользит вниз по склону на расстояние 2,00 м в 2.00 секунд. Найдите (а) величину ускорения блока, (б) величину коэффициент кинетического трения между блоком и плоскости, (c) сила трения, действующая на блок, и (d) скорость блок после прохождения 3 м

(а) d x = при 2 2 м = а (2) 2 а = 1,00 м / с 2	(c) F f = м с F N F F = 0.462 (86,6) F f = 40,0 N
(б) sin 30 = F дюйм dir /100 N cos 30 = F N / 100 Н F в директории = 50,0 N F N = 86,6 N F чистая = m всего a F в директории — F f = 10 (1,00) 50 (м к 86,6) = 10 м к = 0.462	(г) d = а т 2 3 = (1) т 2 т = √6 а = Δv / Δt 1 = Δv / √6 v f = 2,45 м / с

канат 5 канатная

Канат Уокер в беде. Веревка прогибается слишком сильно, что привело к остановке канатоходца 600 Ньютон.Угол тета (слева) равен 30 с относительно вертикали, а фи — 10. Каково натяжение левой и правой сторон веревки?
Поскольку она не ходит, мы знаем сумму сил равен нулю. ΣF x = 0 Так как MS Word не может делать нижний индекс в нижнем индексе, я использую T для натяжения вместо F T при работе с компонентами x и y. T x, L = T x, R sinθ F T, L = sinφ F T, R F T, L = sinφ F T, R / sinθ F T, L = 0,347 F T, R	ΣF y = 0 600N = cosθ F T, L + cosφ F T, R 600N = cosθ (0,347 F T, R ) + cosφ F T, R 600N = 0.300 F T, рэнд + 0,985 F T, рэндов F T, R = 467 Н F T, L = 0,347 F T, R F T, L = 162 Н

канат 5.1-5.6 # 7

Масса электрона 9,11 x 10 ^-31 кг имеет начальную скорость 3 x 10 ⁵ РС.Он движется по прямой, и его скорость увеличивается до 7 x 10 ⁵ м / с на расстоянии 5 см. Предполагая, что ускорение постоянное,

(а) определять сила, действующая на электрон

(б) сравнивать эта сила с весом электрона, которым пренебрегли

г = в 2 + v i т г = (Дв / Дт) т 2 + в i т d = Dv т + в и т d = (v f -v i ) t + v i t t = 2d / (v f + v i ) t = 10 -7 сек	а = Дв / Дт а = (7-3) x 10 5 /10 -7 а = 4 x 10 12 м / с 2	(б) F w = мг F w = (9.11 x 10 -31 ) 10 м / с 2 F w = 9,11 x 10 -30 м / с 2 вес более чем в 10 11 раз меньше, поэтому игнорировать.
	(а) F = ma F = (9,11 x 10 -31 ) 4 x 10 12 F = 3,64 x 10 -18 N

канат 5.7 # 16 (Бонус)

Объект весом 3 кг является движется в плоскости с координатами x и y, заданными как x = (5t ² 1) м / с и y = (3t ³ + 2) м / с. Найдите величину чистой силы, действующей на этот объект при t = 2 сек.

Отв. 112 N

v = dx / dt х = 5т 2 1 год = 3т 3 + 2 v x = 10 t v y = 9 t 2

а = дв / дт x = 10 а y = 18т F x = m a x F y = m a y F x = 3 (10) F y = 3 (18 т)

@ t = 2 сек F x = 30 N F y = 108 N Ф. 2 = F x 2 + F y 2 F = 112 N

канат 5.7 # 23

Масса 1 кг составляет наблюдается ускорение со скоростью 10 м / с ² в направлении 30 к северу от востока. Сила F ₂ , действующая на массу, имеет магнитудой 5 N и направлен на север. Определите величину и направление силы F ₁ , действующей по массе.

F = ma F = 1 (10) F = 10 N F y = 5 N F = (F x 2 + F y 2 ) 1/2 10 = (F x 2 + 5 2 ) 1/2 F x = 8.66 N, N of E

или F x = cosθ F F x = cos 30 (10) F x = 8,66 N, N от E

канат 5.7 # 26

Два объекта соединены легкой струной, которая проходит над шкивом без трения. Нарисуйте диаграммы свободного тела обоих объектов.Если наклон не имеет трения и если m ₁ = 2,00 кг, m ₂ = 6,00 кг и q = 55,0, найдите (а) ускорения объектов, (б) натяжение в строке, и (c) скорость каждого объекта 2,00 с после выпуска от отдыха.

Схема свободного тела	(а) грех 55 = F в реж. /60 N Ф. 2 -в директории = 49.1 N F net = F 2 дюйма, диаметр м 1 g = ma 49,1 с.ш. 20 N = (2 + 6) а а = 3,6 м / с 2 (б) т 1 = м 1 (г + а) т 1 = 2 (9,8 + 3,6) т 1 = 26,8 N Или тяжелый путь !!! т 2 = m 2 (sin 55g — a) т 2 = 6 (грех 55 9.8 — 3,6) т 2 = 26,6 N
		(в) а = Dv / Dt 3,6 = v f / 2 v f = 7,2 м / с

канат 5.8 # 44

Коэффициент кинетического трения, f k , между столом и блоком 1 кг — 0.350. (а) рисовать диаграмма свободного тела каждого объекта (б) определить ускорение каждого объекта & направление (в) определять натяжение обоих шнуров

F F = 0,35 * 1 кг * 10 м / с 2 F F = 3,5 Н Ф 4 = 4 кг * 10 м / с 2 Ф 4 = 40 Н Ф. 2 = 2 кг * 10 м / с 2 Ф. 2 = 20 Н

F Нетто = F 4 F 2 F f F Нетто = m всего a Ф 4 F 2 F f = m всего 40N 20Н 3.5N = (4 + 2 + 1) а а = 2,36 м / с 2

F T4 = m (г а) F T4 = 4 * (10 — 2,36) F T4 = 30,6 N F T2 = м (г + а) F T2 = 2 * (10 + 2.36) F T2 = 24.7 с.ш.

канат 5 # 61

Какой горизонтальный сила должна быть приложена к тележке массы M, показанной ниже, чтобы блоки оставаться неподвижным относительно тележки? (Без трения и безмассовый)
Устройство неподвижного шкива без трения т 1 = Т 2 a 2 = а 1
т 1 = m 1 a т 2 = m 2 г T 1 = T 2 м 1 а 1 = m 2 г а 1 = м 2 г / м 1	а 2 = а 1 а 2 = м 2 г / м 1 F = (M + м 1 + м 2 ) (а 2 ) F = (M + м 1 + м 2 ) (м 2 г / м 1 )

канат 5.8 # 41

Блок 3 кг начинается с отдыха на вершине 30-го уклона и скользит по склону на расстояние 2 м за 1,5 секунд. Найдите (а) величину ускорения блока, (б) величину коэффициент кинетического трения между блоком и плоскостью, (c) фрикционное сила, действующая на блок, и (d) скорость блока после того, как он проскользнул на 2 м.

(а) d x = в 2 2 м = а (1,5) 2 а = 1.78 м / с 2
(б) грех 30 = F в директории /30 N cos 30 = F N /30 N F дюйм dir = 15 N F N = 26 N
F net = F в директории — F f F в директории — F f = m всего a F net = 15 Н (м к 26 Н) 15 — м с 26 = 3 (1.78) м с = 0,372
(в) F F = м с F N F f = 0,372 (26 Н) F f = 9,56 N	г = по телефону 2 г = (Дв / Дт) т 2 d = v f t v f = 2,67 м / с

канат 5.7 # 18

Вес 325 N мешок с цементом висит на трех проводах. Система находится в равновесии. Две проволоки образуют углы q 1 = 60 & q 2 = 25 с горизонтальный. Найдите напряжение в T 1 , Т 2 и Т 3 . Подсказка: Поскольку в равновесии F y = 0 F x = 0 Ответ: T 1 = 296 N, T 2 =?

Дано: Т 3 = 325 Н вверх Силы = Прижимающие силы т 1 sinq 1 + T 2 sinq 2 = T 3 Силы left = принудительно T 1 cosq 1 = T 2 cosq 2 Решить для T 1 т 1 = T 2 cosq 2 / cosq 1

T 1 sinq 1 + T 2 sinq 2 = T 3 T 2 cosq 2 / cosq 1 sinq 1 + T 2 sinq 2 = 325 Н Т 2 1.57 + Т 2 0,42 = 325 Н Т 2 = 163 Н T 1 sinq 1 + T 2 sinq 2 = T 3 T 1 sin60 + 163 (sin25) = 325 Н т 1 = 296 Н

канат 5.7 # 24

Объект весом 5,00 кг помещенный на горизонтальный стол без трения, соединенный с веревкой, которая проходит над шкивом и затем крепится к подвеске 9.Объект 00 кг. (а) Розыгрыш бесплатно схемы тел обоих объектов. (б) Найдите ускорение двух предметов и натяжение струны

(а)

(б) F Нетто = м T F w2 = (m 1 + m 2 ) * a 90 Н = (5 + 9) кг * а = 6.43 м / с 2

9 кг блок падает, поэтому, если он был в лифте и начал опускаться, он весит меньше F T = m (г а) F T = 9 кг (10 6,43) F T = 32,1 N или F T = м F T = 5 (6,43) F T = 32,1 N

канат 5 # 68

Два блоки массы 3.50 кг и 8,00 кг соединены безмассовым струна, проходящая через шкив без трения. Подъемы без трения. Найдите (а) в величина ускорения каждого блока (б) в натяжение струны Для блок 8 кг F в директории = sin 35 мг = 45,0 N Для блок 3,5 кг F в директории = sin 35 мг = 19,7 Н F Net = m всего a (45 19.7) = (8 + 3,5) * а а = 2,2 м / с 2

Натяжение _{на 3,5 кг} = m a = 3,5 кг * (sin 35 g + a) = 3,5 * (7,82) = 27,4 Н

Натяжение _{на 8 кг} = m a = 8 кг * (sin 35 g — a) = 8 * (3,42) = 27.4 с.ш.

канат 5 # 69

Микроавтобус ускоряется спуск с холма, выход из состояния покоя до 30 м / с за 6 сек.При разгоне игрушка массой 0,1 кг висит на веревке с потолка фургона. Ускорение таково, что струна остается перпендикулярной к потолок. Определите а) угол θ, б) натяжение струны.

а) а = Дв / Дт а = (300) / 6 а = 5 м / с 2	грех θ = ма / мг грех θ = 5 / 9,8 θ = 30.7˚
(б) cos θ = Т / мг т = 0.84 N

канат 5 Блок массы m = 2 кг опирается на левый край блока большей массы м = 8 кг.

Коэффициент кинетического трения между двумя блоками составляет 0,3, и поверхность, на которой лежит блок весом 8 кг, не имеет трения. Постоянная горизонтальная сила величиной F = 10 Н прикладывается к блоку 2 кг, приводя его в движение, как показано выше. Если длина L, то передний край меньшего блока перемещается по большему блоку составляет 3 м (а) как Пройдет много времени, прежде чем этот блок доберется до правой стороны от 8 кг блокировать? (б) Как далеко перемещается 8-килограммовый блок в процессе? Ответ 2.13с, 1.67м

(a) Вы применяете Усилие 10 Н на блоке 2 кг. Трение противостоит приложенная сила 10 Н. F F = м Н F F = .3 (мг) F F = .3 (20Н) F F = 6 Н	F Net = F применяется Ф Ф F Net = m a F Нетто = 10 6 F Net = 4 N F Нетто = м верх 4 Н = (2 кг) верх a верх = 2 м / с 2	ньютонов 3 rd закон гласил, что для каждое действие (Фрикционный сила нижнего блока на верхнем блоке) существует равная и противоположная реакция (сила трения верхнего блока на нижний блок) . F снизу = — Ftop блок F снизу = 6 Н вправо
F низ = м низ a дно 6N = 8 кг днище a дно = м / с 2 (используйте b для снизу, т для верха)	(б) г б = a b t 2 + v o t + d b г б = т 2 + 0 + 0 г б = 3т 2 /8 г б = 3 (24/5) / 8 г б = 1.8м	(а) d t = a t t 2 + v o t + d o 3 + d b = 2t 2 + 0 + 0 3 + 3т 2 /8 = 2т 2 + 0 + 0 3 = 5 т 2 /8 т = 2,19 с
(б) а = Дв / Дт 0,75 = Dv / 2,19 с v f = 1.64 м / с

канат 5 5 ^-е издание 77 дополнительная проблема

До 1960 г. считал, что максимально достижимый коэффициент статического трения для автомобиля шина была меньше 1. Тогда примерно в 1962 г. три компании независимо друг от друга разработали гоночные шины с коэффициентами 1.6. С тех пор шины улучшились, так как проиллюстрировано в этой задаче. Согласно в Книгу рекордов Гиннеса 1990 года, время голодания, когда поршневой двигатель карта изначально в состоянии покоя преодолела расстояние в 4 мили.96с. Этот рекорд был установлен Ширли Малдауни в сентябре 1989 года. а) Если предположить, что задние колеса почти приподняли передние колеса над дорожным покрытием, какое минимальное значение m _s нужно добиться рекордного времени?

б) Предположим, Малдауни удалось удвоить мощность двигателя, сохранив при прочих равных. Как бы это изменение влияет на прошедшее время?

1 миля = 1609 м (задняя обложка книги)

v ср. = Δx / Δt против ср. = (* 1609) / 4.96 (v и + v f ) = (1609/4) / 4,96 v f = 162,2 м / с	F F м с N F f = m s мг Применяя крутящий момент вокруг задних колес эффективный м с может превышать 1 F f = F Net F f = m s мг F Net = ma	м с мг = ма м с г = м с = 32.7/10 м с = 3,27
а = Дв / Дт а = (162,2 0) / 4,96 с а = 32,7 м / с		г. Любая дополнительная мощность вредна (автомобиль переверните назад, иначе колеса начнут вращаться) и увеличьте время

4 ключевых способа повысить напряжение и темп в вашей художественной литературе

В этом месяце мы рассмотрели темп и напряжение, фатальный недостаток № 7 писателя-беллетриста.Писателям не всегда легко оценить это в своих сценах. Как узнать, затягивается ли ваша сцена и нет ли напряжения?

Четыре наших редактора нашли отличные способы повысить напряжение и темп в новых сценах. Повторюсь, вот несколько ключевых моментов:

1) Внутренний и внешний конфликт. Во-первых, вы хотите, чтобы ваши страницы были доведены до краев конфликтами. Значимый конфликт. Показывать, что персонаж суетится на целую страницу из-за своего паршивого маникюра, не имеет особого смысла.

Так вот, эта ситуация могла быть центром по-настоящему веселого комедийного момента, а если так, то потрясающего. Юмор — отличный юмор — так часто упускается из виду, он ускоряет темп и привлекает читателей. Но не все романы полны забавных моментов.

Конфликт — это напряжение. Значимый конфликт создает сильное напряжение. Хемингуэй сказал: «Не путайте движение с действием». То, что у вас много чего происходит, с точки зрения сюжета, еще не означает, что что-то действительно происходит. У вас может быть масса захватывающих автомобильных погонь, авиакатастроф и перестрелок, и читатель может засыпать, уткнувшись носом в вашу книгу.

Итак, убедитесь, что вы везде, где возможно, обеспечиваете значимый внутренний и внешний конфликт. Чем больше вы можете усложнить жизнь своим персонажам, тем больше потенциального напряжения. Покажите, как ваши персонажи борются изнутри и снаружи. Но эта тема всегда возвращает меня к ключевому фактору создания напряженности.

2) Интересные персонажи. Если я сказал это однажды, я сказал это тысячу раз: если читатели не заботятся о ваших персонажах, заботятся о том, что с ними происходит, они не почувствуют этого напряжения.Мы хотим, чтобы наши читатели были напряжены. Обеспокоенный, озабоченный, приклеенный к странице, с нетерпением ожидая того, что будет дальше. Они не почувствуют этого напряжения, если вы не проделаете тяжелую предварительную работу по развитию, а затем с самого начала оживили этих чутких, уникальных, неотразимых персонажей.

Да, у вас может получиться отличный сюжет. Захватывающий, захватывающий, оригинальный сюжет. Но если ваши персонажи скучные, неинтересные, приземленные, раздражающие, лишенные страсти, навыков или интереса к чему-либо, или , все великие повороты сюжета в мире не вызовут напряженности.

Если вы можете принести домой одну ключевую информацию о напряжении и ритме, сделайте это.

3) Не забивайте сцены скучными вещами. Что скучно? Все, что не интересно. Мне не нужно объяснять это, верно? Когда вы читаете роман и замечаете, что засыпаете, думая о том, что приготовить на ужин, пролистывая страницы, которые, как вы позже понимаете, вы, возможно, читали, но не можете вспомнить, вы знаете, что просто попали в скучный участок.

Это может быть применено к макро- и микро-проблемам.Вам не нужны скучные сцены — персонажи, сидящие в унылой, неинтересной обстановке (некоторые из вас знакомы с моей тирадой о слишком большом количестве сцен в Starbuck’s или ресторанах, где персонажи просто разговаривают и пьют кофе).

Каждая сцена должна иметь четкую, важную цель в продвижении и / или усложнении вашего сюжета. Вашему герою будет сложнее достичь своей цели. Обычно причина того, что во многих сценах первых романов отсутствует напряжение и темп, заключается в том, что ничего не происходит.Мы исследовали все это в феврале, когда рассматривали Fatal Flaw # 2: Nothin ’Happenin’.

Пройдите свой WIP (работа в процессе). Избавьтесь от каждой сцены, в которой ничего не происходит. Или переделайте так, чтобы произошло что-то значимое. Я не могу достаточно подчеркнуть, насколько важен этот план сцены. Вот почему я создал этот контрольный список сцены и шаблон структуры сцены. Подумайте об использовании их для каждой сцены.

Я могу гарантировать вам: если вы убедитесь, что каждая сцена важна для вашей истории и способствует развитию сюжета, вы обнаружите, что ваш темп и напряжение нарастают.

На микроуровне посмотрите на свое письмо. Большинство романов, которые я редактирую и критикую, наполнены посторонними словами, которые перетаскивают. Представьте, что каждое слово имеет определенный вес и что ваши читатели несут ваши сцены по крутому склону. Чем тяжелее мешок слов, который они несут, тем труднее добраться до вершины.

Если бы я взбирался на этот холм, а мешок был бы слишком тяжелым, я бы остановился, сел и вывалил его содержимое на землю. Затем перебери все эти слова и выбрось столько, сколько смогу, что мне действительно не нужно.Часто можно выбросить четыре в обмен на одно хорошее слово. Считайте каждое слово. Ваш читатель поднимется к кульминации вашей истории более легким и счастливым шагом.

Напряжение и темп — одна из основополагающих принципов нового строительства. Если вам нужно узнать больше, прочитайте сообщения из прошлогоднего курса по напряжению. Они напряженные. А если вы купите и воспользуетесь учебным пособием «12 ключевых столпов нового строительства», вам будет предложено создать все необходимое напряжение, чтобы ваш роман разгорелся.

4) Потратьте время на разработку фирменного стиля письма. Может быть, вы не думали, что это может повлиять на ритм и напряжение, но это действительно так. Это снова связано со словом «скучно». Если вы используете лишенные воображения слова, фразы, описания, повествования, вам придется работать намного усерднее, чтобы удержать интерес вашего читателя. Ваш сюжет, персонажи и другие компоненты романа должны будут нести на себе всю тяжесть напряжения и ритма.

Напротив, в сюжете часто может происходить очень мало событий.И да, я пойду так далеко, что скажу, что вы даже можете превратить эту скучную сцену в том скучном ресторане в захватывающее и напряженное переживание для вашего читателя, если вы пишете эффектно. Я имею в виду, что ваша проза прекрасна; ваш выбор слов свеж и удивителен; ваши концепции и аннотации оригинальны и полностью новы; а ваши метафоры, мотивы, символика и сравнения волнуют и заставляют задуматься.

Нет, вряд ли вы будете удивлять читателя каждой строчкой, но почему бы не стремиться к тому, чтобы каждая страница отражала твердое понимание творческого использования языка.Поставьте перед собой цель стать прекрасным мастером слова, составлять красивые предложения так, как скульптор или художник обращается с мрамором или краской. Пустая страница — это ваш холст, а слова, которые вы пишете и впоследствии публикуете, демонстрируют миру ваш талант и креативность. Не рисуйте скучные картинки со словами, если вы можете сделать гораздо больше, чем просто набросать слова на страницу, не задумываясь.

Последний комментарий по поводу стимуляции. Настойчивый темп на протяжении всей книги не означает, что все должно двигаться со скоростью света.Не путайте темп со скоростью. У вас должны быть медленные, задумчивые моменты с вашими персонажами. Романы представляют собой цикл действие-реакция-действие-реакция. Что-то случается, персонажи реагируют, обрабатывают, принимают решения (действуют), а затем происходит еще что-то.

В эти задумчивые моменты можно подумать, что темп замедлился. Автомобильная погоня окончена, и теперь герой сидит в кресле в больнице и смотрит на любимую женщину, которая находится в коме. Конечно, действие замедлилось, помните Хемингуэя: движение не означает действие.Точно так же отсутствие движения не означает бездействия. Острая, тяжелая эмоциональная сцена, в которой мало действий, может быть столь же напряженной или даже намного более напряженной, чем эта скоростная автомобильная погоня. Почему? Потому что вы заставили своих читателей эмоционально погрузиться в ваших персонажей. Есть смысл?

Вы, наверное, не представляли, что в художественной литературе так много темпов и напряженности. Я надеюсь, что исследование, проведенное в этом месяце, поможет вам обнаружить эти недостатки в вашей художественной литературе (а также в романах и рассказах, которые вы читаете) и исправить их так, чтобы ваши сцены шипели от напряжения, а ваши читатели продолжали перелистывать страницы, желая знать, что будет дальше.

Ваша очередь:

Что заставляет вас напрягаться при чтении романа? Что для вас замедляет темп? Есть мысли о том, как лучше всего создать напряжение в ваших сценах? Хотите поделиться тем, что вы сделали, чтобы усилить темп и напряжение в скучной сцене?

Сил в двух измерениях — Практика — Физика Гипертекст

Применить второй закон движения Ньютона…

∑ F = м a

, но сделайте это дважды.(Пусть вверх и вперед будут положительные направления.)

В горизонтальном направлении горизонтальная составляющая натяжения неуравновешена. Это чистая сила.

∑ F x	=	ма x
T sin θ	=	ma

В вертикальном направлении мы предполагаем, что ускорение отсутствует.Восходящий компонент натяжения должен уравновешивать нисходящий вес маятникового боба.

∑ F y	=	ma y
T cos θ — мг	=	0
T cos θ	=	мг

Разделите эти два уравнения.

T sin θ	=	ma
T cos θ		мг

Упростите, используя алгебру и триггерные тождества.

a = г tan θ

Проверьте уравнение с несколькими репрезентативными значениями. Угол 0 ° означает отсутствие ускорения, поскольку tan 0 ° = 0; угол 45 ° соответствует горизонтальному ускорению в 1 g, поскольку tan 45 ° = 1; и угол 90 ° невозможен, так как tan 90 ° = ∞.

Хотя идея использования маятника для измерения горизонтального ускорения проста, действительно не было необходимости в ее создании, пока люди не начали регулярно двигаться со скоростью, превышающей быструю лошадь. Первый маятниковый акселерометр был построен в 1889 году британским инженером-механиком Фредериком Ланчестером (1868–1946). К маятнику был прикреплен карандаш, чтобы он мог автоматически рисовать график ускорения-времени на листе бумаги.

→ время → Поезд 1889: (а) (б) (г) (д) торможение; (c) начиная с

← время ← Автомобиль 1905 года: верх и низ, трогание с места и остановка; средний, стартовый и выбегающий

Компания Lanchester интересовалась плавностью работы тормозных систем в поездах.В частности, его интересовала причина резкого изменения движения, которое происходит прямо перед тем, как тормозящий поезд останавливается.

Замечено, что характерной чертой тормозных диаграмм является внезапность падения в момент остановки. Это очень интересный и важный момент, поскольку он является причиной «рывка», который почти всегда возникает, когда поезд останавливается; Собственно, при исследовании этого рывка в 1888 году писателю пришла в голову идея маятникового акселерометра.В то время предполагалось, что рывок был результатом отдачи буферных пружин после остановки; тогда как очень небольшое рассмотрение показывает, что на самом деле именно внезапное изменение ускорения на [выделено оригиналом] мы физиологически распознаем как «рывок», то есть df / dt [по какой-то странной причине он решил использовать f для ускорения], а не изменения направления движения. Фактически само собой напрашивается, что термину «рывок» можно было бы придать научное значение и определить его как d ³ s / dt ³ .