Мдп что это: Система МДП | IRU | World Road Transport Organisation

Система МДП | IRU | World Road Transport Organisation

Что Вы ищете..?

введите запрос выше

Выберите язык

1. Главная
2. Что мы делаем
3. Упрощение процедур торговли и транзита
4. Система МДП

По всему миру. Уверенно. Надежно.

МДП – это единственная в мире система международного таможенного транзита. 

Она позволяет перевозить товары из страны отправления в страну назначения в опечатанных грузовых отделениях, которые проходят таможенный контроль через многостороннюю, взаимно признанную систему. Это самый простой, безопасный и надежный способ перемещения товаров через несколько международных границ, что экономит время и деньги для транспортных операторов и таможенных органов.

Что такое МДП

Система МДП упрощает процедуры на границах, уменьшая административную нагрузку на таможенные органы и транспортно-логистические компании. Это значительно сокращает время ожидания на границе, экономя время и деньги.

Подробнее

Глобальный охват системы МДП

К Конвенции МДП уже присоединились 77 договаривающихся сторон по всему миру, и их число быстро растет — более 20 стран рассматривают возможность присоединения к Конвенции.

Подробнее

Функционирование системы МДП

Система МДП позволяет перевозить товары из страны отправления в страну назначения в опечатанных грузовых отделениях, которые проходят таможенный контроль через многостороннюю, взаимно признанную систему.

Подробнее

Цифровизация системы МДП

eTIR позволяет обеспечить совместимость функциональных возможностей системы и других цифровых процедур в мультимодальных сферах логистики, транспорта, электронных таможенных услуг и в других соответствующих областях.

Подробнее

Публикации МДП

Отчеты, брошюры и другие документы, относящиеся к МДП

Подробнее

Гарантии МДП

Каждая перевозка по процедуре МДП защищена гарантией на сумму до 100 тыс. евро. См. полный список пределов гарантий во всех странах.

Подробнее

Несколько фактов о системе МДП

• сокращает сроки перевозки до 80% и расходы до 38%;
• более 30 000 транспортных и логистических компаний используют МДП для быстрого и надежного перемещения товаров через международные границы;
• 1 млн. МДП транзитов в год;
• используется единая гарантия, позволяющая операторам перемещать товары в пути через любые страны МДП;
• Управление системой МДП осуществляет IRU на основании мандата, выданного ООН;
• международная гарантия распространяется на все таможенные пошлины и налоги, подверженные риску, с максимальной защитой 100 000 евро за транспортную операцию;
• является эффективным инструментом для осуществления Соглашения Всемирной торговой организации по упрощению процедур торговли и пересмотренной Киотской конвенции;
• соответствует Рамочной программе SAFE Всемирной таможенной организации.

Загрузить буклет

Успешное государственно-частное партнерство с ООН

Готовы присоединиться к МДП?

Остались вопросы? Свяжитесь с департаментом МДП

Что такое МДП? | IRU

Справочная информация о системе МДП

Более 70 лет IRU способствует экономическому росту, процветанию и безопасности. 

Сегодня IRU — ведущая организация в области автомобильных перевозок и упрощения процедур торговли и транзита, которая представляет интересы более 3,5 млн транспортных операторов из более чем 80 стран.

В 1948 году IRU учреждался с идеей вдохнуть новую жизнь в разрушенные войной торговлю и коммерческие связи европейских стран за счет упрощения транзита пассажиров и грузов. С этой цель был создан альянс национальных ассоциаций автомобильных перевозчиков грузов и пассажиров восьми европейских стран. Это позволило отстаивать интересы отрасли в недавно сформированной Европейской экономической комиссии Организации Объединенных Наций, в задачи которой входила разработка нормативно-правовой базы для новой послевоенной Европы.

На фоне неустойчивости границ и ненадежности геополитических отношений возникла необходимость в решении, которое бы позволило вновь наладить торговлю в Европе и, таким образом, помочь восстановиться экономике и населению.

И такое решение было найдено IRU. Система таможенного транзита МДП стала основой для беспрепятственных международных перевозок грузов и пассажиров.

Новая система была предназначена для упрощения и ускорения процедур торговли за счет отправки грузов из страны происхождения в страну назначения через страны транзита в опломбированных грузовых отделениях, таможенный контроль которых опирается на многостороннюю систему, признанную всеми сторонами.

Мандат на управление системой МДП ООН вручила признанному лидеру в области автомобильного транспорта — IRU. За 70 лет система МДП из локальной договоренности выросла в единственную глобальную международную систему таможенного транзита и гарантий.

Сегодня системой МДП пользуются 77 договаривающихся сторон Конвенции МДП. Ежегодно почти миллион книжек МДП выдается более 10 тыс. транспортных и логистических предприятий. Ежемесячно перевозки в соответствии с процедурой МДП по всему миру осуществляют 80 тыс. грузовых транспортных средств.

Современные грузы, которые перевозятся на основании книжки МДП, покрываются единой международной гарантией от начала до конца перевозки, даже когда речь идет об интермодальных транспортных операциях. Это простой, безопасный и надежный способ перемещения грузов через границы — как в рамках прямых двусторонних перевозок между сопредельными странами, так и по более сложным маршрутам, пролегающим через несколько стран.

Что дальше?

При жизни следующего поколения объем автомобильных перевозок, которые будут как заменять, так и дополнять железнодорожный, воздушный и морской транспорт, существенно возрастет. МДП станет одним из ключевых благоприятных факторов развития автомобильных перевозок и основой экологически чистых и устойчивых автотранспортных сетей. IRU как администратор системы продолжит в сотрудничестве с ООН работать над привлечением новых договаривающихся сторон в целях расширения базы знаний и области действий. Обладая более чем 70-летним опытом в области мобильности и логистики, IRU по-прежнему является мировым экспертом в вопросах пересечения государственных границ.

Марковский процесс принятия решений Определение, работа и примеры

Марковский процесс принятия решений (MDP) определяется как стохастический процесс принятия решений, который использует математическую основу для моделирования принятия решений динамической системой в сценариях, где результаты либо случайны, либо контролируются лицом, принимающим решения, которое принимает последовательные решения с течением времени. Эта статья объясняет MDP с помощью некоторых реальных примеров.

Содержание

• Что такое марковский процесс принятия решений?
• Как работает марковский процесс принятия решений?
• Примеры марковского процесса принятия решений

Что такое марковский процесс принятия решений?

Марковский процесс принятия решений (MDP) относится к стохастическому процессу принятия решений, который использует математическую основу для моделирования принятия решений динамической системой. Он используется в сценариях, где результаты либо случайны, либо контролируются лицом, принимающим решения, которое принимает последовательные решения с течением времени. MDP оценивают, какие действия следует предпринять лицу, принимающему решения, с учетом текущего состояния и среды системы.

MDP полагаются на такие переменные, как среда, действия агента и вознаграждения, чтобы определить следующее оптимальное действие системы. Они подразделяются на четыре типа — конечные, бесконечные, непрерывные или дискретные — в зависимости от различных факторов, таких как наборы действий, доступные состояния и частота принятия решений.

MDP существуют с начала 1950-х годов. Имя Марков относится к русскому математику Андрею Маркову, сыгравшему ключевую роль в формировании случайных процессов. Известно, что в первые дни MDP решали проблемы, связанные с управлением и контролем запасов, оптимизацией очередей и вопросами маршрутизации. Сегодня MDP находят применение при изучении задач оптимизации с помощью динамического программирования, робототехники, автоматического управления, экономики, производства и т. д.

В искусственном интеллекте MDP моделируют последовательные сценарии принятия решений с вероятностной динамикой. Они используются для разработки интеллектуальных машин или агентов, которые должны работать дольше в среде, где действия могут привести к неопределенным результатам.

Модели MDP обычно популярны в двух областях ИИ: вероятностном планировании и обучении с подкреплением (RL).

• Вероятностное планирование — это дисциплина, использующая известные модели для достижения целей и задач агента. При этом он делает упор на то, чтобы направлять машины или агентов к принятию решений, позволяя им научиться вести себя для достижения своих целей.
• Обучение с подкреплением позволяет приложениям учиться на обратной связи, которую агенты получают из среды.

Давайте разберемся с этим на примере из реальной жизни :

Рассмотрим голодную антилопу в заповеднике дикой природы, ищущую пищу в окружающей среде. Натыкается на место с грибом справа и цветной капустой слева.

Если антилопа съест гриб, в награду она получит воду. Однако, если он выберет цветную капусту, ближайшая клетка со львом откроется и освободит льва в святилище. Со временем антилопа учится выбирать сторону гриба, поскольку взамен этот выбор предлагает ценную награду.

В приведенном выше примере MDP существуют два важных элемента — агент и среда. Агентом здесь является антилопа, которая действует как лицо, принимающее решения. Окружающая среда показывает окружение (заповедник дикой природы), в котором обитает антилопа. Поскольку агент выполняет разные действия, возникают разные ситуации. Эти ситуации называются состояниями. Например, когда антилопа выполняет действие поедания гриба, она получает награду (воду) в соответствии с действием и переходит в другое состояние. Агент (антилопа) повторяет процесс в течение определенного периода и изучает оптимальное действие в каждом состоянии.

В контексте MDP мы можем формализовать, что антилопа знает оптимальное действие для выполнения (съесть гриб).

Поэтому он не предпочитает есть цветную капусту, поскольку она приносит вознаграждение, которое может повредить его выживанию. Пример показывает, что MDP имеет важное значение для фиксации динамики проблем RL.

Узнать больше: Что такое HCI (взаимодействие человека и компьютера)? Значение, важность, примеры и цели

Как работает марковский процесс принятия решений?

Модель MDP работает с использованием ключевых элементов, таких как агент, состояния, действия, вознаграждения и оптимальные политики. Агент относится к системе, ответственной за принятие решений и выполнение действий. Он работает в среде, подробно описывающей различные состояния, в которых находится агент, когда он переходит из одного состояния в другое. MDP определяет механизм того, как одни состояния и действия агента приводят к другим состояниям. Более того, агент получает вознаграждение в зависимости от выполняемого им действия и достигнутого им состояния (текущего состояния).

Политика для модели MDP раскрывает следующие действия агента в зависимости от его текущего состояния.

Платформа MDP имеет следующие ключевые компоненты:

• S : состояния ( s ∈ S )
• A : Действия (a ∈ A )
• P (S T+1 | S T .A T ) : вероятности перехода
• R (с) : Награда

Графическое представление модели MDP выглядит следующим образом:

Модель MDP использует свойство Маркова, которое гласит, что будущее можно определить только из настоящего состояния, которое инкапсулирует всю необходимую информацию из прошлого. Свойство Маркова можно оценить с помощью следующего уравнения:

P[S t+1 |S t ] = P[S t+1 9000 4 |S 1 ,S 2 ,S 3 ……S t ]

Согласно этому уравнению вероятность следующего состояния (P[S t+1 ]) при текущем состоянии (S t ) дается вероятность следующего состояния (P[S t+1 ]) с учетом всех предыдущих состояний (S 1 ,S 2 , S 3 ……S т ) . Это означает, что MDP использует только настоящее/текущее состояние для оценки следующих действий без каких-либо зависимостей от предыдущих состояний или действий.

Функция политики и значения

Известно, что политика ( Π) определяет оптимальное действие агента с учетом текущего состояния, чтобы он получил максимальное вознаграждение. Проще говоря, он связывает действия с состояниями.

Π: S -> A

Чтобы определить наилучшую политику, важно определить доходность, которая раскрывает вознаграждение агента в каждом состоянии. В результате метод горизонта не предпочтительнее, поскольку он фокусируется на краткосрочных или долгосрочных вознаграждениях. Вместо этого вводится переменная под названием «дисконтированный фактор (γ)». Правило гласит, что если γ имеет значения, близкие к нулю, то приоритет отдается немедленным вознаграждениям. Впоследствии, если γ показывает значения, близкие к единице, то акцент смещается на долгосрочное вознаграждение. Следовательно, метод дисконтированного бесконечного горизонта является ключом к выявлению наилучшей политики.

Функция значения В(с) определяет возврат вознаграждения в каждом конкретном состоянии. Его формула характеризуется ожидаемой суммой дисконтированных будущих вознаграждений:

Ценностную функцию можно разделить на две составляющие: вознаграждение текущего состояния и дисконтированное значение вознаграждения следующего состояния. Эта разбивка дает уравнение Беллмана, как показано ниже:

Здесь стоит отметить, что действия и вознаграждения агента зависят от политики. Это означает, что функция ценности специфична для политики.

Функция оптимального значения может быть решена с помощью итерационных методов, таких как оценки методом Монте-Карло, динамическое программирование или обучение на основе временных разностей. Политика, которая выбирает максимальное оптимальное значение с учетом текущего состояния, называется оптимальной политикой. Математически это представлено следующим уравнением:

Таким образом, политика является следствием текущего состояния, при этом на каждом временном шаге новая политика оценивается на основе информации о текущем состоянии. Это возможно с помощью нескольких методов, таких как итерация политики, Q-обучение, итерация значений и линейное программирование для решения оптимальной функции политики.

Давайте теперь посмотрим на реальный пример, чтобы лучше понять работу MDP:

У нас есть проблема, в которой нам нужно решить, должны ли племена охотиться на оленей или нет в близлежащем лесу, чтобы обеспечить долгосрочную прибыль. Каждый олень приносит фиксированную прибыль. Однако, если племена охотятся сверх лимита, это может привести к более низкому урожаю в следующем году. Следовательно, нам нужно определить оптимальную долю оленей, которую можно поймать, получая при этом максимальную отдачу в течение более длительного периода.

Постановка задачи в этом случае может быть упрощена: охотиться на определенную часть оленей или нет. В контексте MDP проблема может быть выражена следующим образом:

Штаты : Количество оленей в лесу в рассматриваемом году. Четыре состояния включают пустое, низкое, среднее и высокое, которые определяются следующим образом:

• Пусто : Олени недоступны для охоты
• Низкий : Доступное количество оленей ниже порогового значения t_1
• Средний : Доступное количество оленей между t_1 и t_2
• Высокий : Доступное количество оленей превышает пороговое значение t_2

Действия : Действия включают go_hunt и no_hunting, где go_hunt подразумевает отлов определенного количества оленей. Важно отметить, что для пустого состояния единственным возможным действием является no_hunting.

Награды : Охота в каждом штате приносит определенные награды. Награды за охоту в разных штатах, таких как низкий, средний и высокий, могут быть 5000 долларов, 50000 долларов и 100000 долларов соответственно. Более того, если действие приводит к пустому состоянию, вознаграждение составляет -200 тысяч долларов. Это связано с необходимостью электронного разведения новых оленей, что требует времени и денег.

Переходы состояний : Охота в состоянии вызывает переход в состояние с меньшим количеством оленей. Впоследствии действие no_hunting вызывает переход в состояние с большим количеством оленей, за исключением «высокого» состояния.

Подробнее: Что такое дерево решений? Алгоритмы, шаблоны, примеры и лучшие практики

Примеры марковского процесса принятия решений

MDP внесли значительный вклад в несколько прикладных областей, таких как информатика, электротехника, производство, исследование операций, финансы и экономика, телекоммуникации и т. д. на.

Ниже перечислены несколько простых примеров, в которых MDP продолжает играть неизбежную роль:

1. Проблемы маршрутизации

Последовательное принятие решений на основе MDP используется для решения проблем маршрутизации, таких как выявленные в задаче коммивояжера (TSP). ). TSP можно разбить на следующие компоненты:

• Продавец = агент,
• Доступные маршруты = действия, которые агент может выполнять в текущем состоянии,
• вознаграждений = затраты на прохождение определенных маршрутов и 
• Цель = оптимальная политика, снижающая общую стоимость на все время поездки.

2. Управление обслуживанием и ремонтом динамических систем

Проблемы с обслуживанием и ремонтом относятся к динамическим системам, таким как автомобили, автобусы или грузовики, которые со временем изнашиваются из-за действий в различных условиях. Решения в этом случае могут относиться к бездействию, выполнению задач по ремонту или замене критических компонентов транспортного средства. Постановка этой задачи в рамках MDP позволяет системе выбирать действия, которые помогают минимизировать затраты на техническое обслуживание автомобиля в течение всего срока его службы.

3. Проектирование интеллектуальных машин

Достижения в области искусственного интеллекта и машинного обучения привели к широкому использованию MDP в робототехнике, сложных автономных системах, автономных транспортных средствах, автоматизированных системах и т. д. MDP используются в моделях обучения с подкреплением, которые учат роботов и машины тому, как автономно учиться и выполнять определенные задачи.

Например, DeepMind Technologies, дочерняя компания Google, объединяет платформу MDP с нейронными сетями и обучает вычислительные системы играть в игры Atari лучше, чем люди. Компания также использовала MDP для обучения машин играть в настольные игры, такие как AlphaGo. DeepMind Technologies также использовала платформу MDP для обучения смоделированных роботов ходьбе и бегу.

4. Разработка игр-викторин

MDP широко используются для разработки игр-викторин с определенными уровнями. На каждом уровне задается вопрос, правильный ответ на который приносит денежное вознаграждение. По мере повышения уровня вопросы усложняются и влекут за собой более высокие награды.

В играх-викторинах, если участник хорошо играет и правильно отвечает на все вопросы, то он получает за это вознаграждение, а также возможность решить, играть ли викторину оттуда или выйти из игры. Если участник выходит, он, возможно, может сохранить все заработанные награды. Однако, если он решит играть и не сможет правильно ответить на вопрос на определенном уровне, он потеряет все накопленные награды. Цель таких игр — оценить действия по игре или выходу из нее при максимальном вознаграждении.

5. Управление временем ожидания на перекрестке

MDP помогают определить продолжительность работы светофора. Цель здесь состоит в том, чтобы максимизировать количество транспортных средств, которые могут проехать через транспортные развязки, сохраняя при этом контроль времени их ожидания. Это может быть перекресток с двусторонним движением, где движение может проходить в любом направлении, например, на запад или на юг, и так далее. Также предполагается наличие в системе данных о количестве автомобилей, подъезжающих к перекрестку с помощью датчиков. Светофоры в этом случае красные и зеленые. Здесь каждый шаг занимает несколько секунд (2 или 5). С MDP вы можете решить, следует ли менять светофор в зависимости от транспортных средств на перекрестке и времени их ожидания.

6. Определение количества пациентов для госпитализации

Ежедневно определенное количество пациентов посещают больницу по разным причинам. Затем больница должна решить, сколько пациентов она может принять, учитывая такие факторы, как:

• количество уже госпитализированных пациентов,
• количество доступных кроватей и
• — общее количество пациентов, которые выздоравливают и выписываются ежедневно.

Определяя количество пациентов для госпитализации, больница также намеревается максимизировать количество пациентов, которые выздоравливают в течение определенного периода. Обе эти цели могут быть достигнуты путем разработки для них MDP.

Помимо приведенных выше примеров из реальной жизни, MDP жизненно важны для оптимизации телекоммуникационных протоколов, упрощения торговли акциями и тонкой настройки управления очередями в производственных секторах.

См. Больше : Линейная регрессия против логистической регрессии: понимание 13 ключевых различий

Takeaway

Процесс принятия решений Маркова является стохастическим инструментом принятия решений на основе принципа свойства Марков. Он используется для принятия оптимальных решений для динамических систем с учетом их текущего состояния и среды, в которой они работают. MDP является ключевым компонентом приложений для обучения с подкреплением и широко используется для разработки интеллектуальных систем. Несколько отраслей, таких как роботизированная автоматизация процессов, производство, финансы и экономика и логистика, регулярно используют MDP для выполнения своих повседневных задач.

Помогла ли вам эта статья понять марковский процесс принятия решений и его роль в ИИ? Прокомментируйте ниже или дайте нам знать на Facebook Открывает новое окно , Twitter Открывает новое окно 9000 3 или LinkedIn Открывает новое окно . Мы хотели бы услышать от вас!

ПОДРОБНЕЕ ОБ ИСКУССТВЕННОМ ИНТЕЛЛЕКТЕ

• Что такое NoSQL? Особенности, типы и примеры
• Что такое анализ методом конечных элементов? Работа, программное обеспечение и приложения
• Что такое метавселенная? Значение, особенности и важность
• Что такое когнитивная наука? Значение, методы и приложения
• Что такое пространственный анализ? Определение, работа и примеры

Объяснение процесса принятия решений по Маркову | Построен в

Марковский процесс принятия решений (MDP) представляет собой математическую основу, используемую для моделирования задач принятия решений, когда результаты являются частично случайными и частично контролируемыми. Это структура, которая может решить большинство проблем обучения с подкреплением (RL).

Что такое марковский процесс принятия решений?

Марковский процесс принятия решений (MDP) — это математический инструмент, используемый для задач принятия решений, когда результаты частично случайны и частично контролируемы.

Я собираюсь описать проблему RL в широком смысле, и я буду использовать примеры из реальной жизни, оформленные как задачи RL, чтобы помочь вам лучше понять ее.

Вот что мы рассмотрим:

1. Марковская терминология процесса принятия решений.
2. Что такое марковское свойство?
3. Объяснение марковского процесса.
4. Марковский процесс вознаграждения (MRP).
5. Марковский процесс принятия решений (MDP).
6. Возврат ( G_t ).
7. Полис ( π ).
8. Функции значений.
9. Функции оптимального значения марковского процесса принятия решений.

 

Марковская терминология процесса принятия решений

Прежде чем мы перейдем к MDP, нам необходимо рассмотреть несколько важных терминов, которые будут использоваться в этой статье: 

1. Агент: Агент обучения с подкреплением — это сущность, которую мы обучаем принимать правильные решения. Например, робота, которого обучают передвигаться по дому, не разбиваясь.
2. Среда: Среда — это среда, с которой взаимодействует агент. Например, дом, в котором движется робот. Агент не может манипулировать окружающей средой; он может контролировать только свои собственные действия. Другими словами, робот не может контролировать, где в доме стоит стол, но может ходить вокруг него.
3. Состояние: Состояние определяет текущую ситуацию агента. Это может быть точное положение робота в доме, расположение его двух ног или его текущая поза. Все зависит от того, как вы решите проблему.
4. Действие: Выбор, который делает агент на текущем временном шаге. Например, робот может двигать правой или левой ногой, поднимать руку, поднимать предмет или поворачивать вправо/влево и т. д. Мы заранее знаем набор действий (решений), которые может выполнить агент.
5. Политика: Политика — это мыслительный процесс, лежащий в основе выбора действия. На практике это распределение вероятностей, назначенное набору действий. Высоко вознаграждающие действия будут иметь высокую вероятность, и наоборот. Если у действия низкая вероятность, это не значит, что оно вообще не будет выбрано. Просто вероятность того, что его выберут, меньше.

Мы начнем с основной идеи свойства Маркова, а затем продолжим более сложные уровни.

 

Что такое марковское свойство?

Свойство Маркова | Изображение: Rohan Jagtap

Представьте, что робот, сидящий на стуле, встал и выставил правую ногу вперед. Итак, в данный момент он стоит правой ногой вперед. Это его текущее состояние.

Теперь, согласно марковскому свойству, текущее состояние робота зависит только от его непосредственно предшествующего состояния (или предыдущего временного шага), т.е. состояния, в котором он находился, когда встал. И, видимо, не зависит от своего предшествующего состояния — сидящего на стуле. Точно так же его следующее состояние зависит только от его текущего состояния.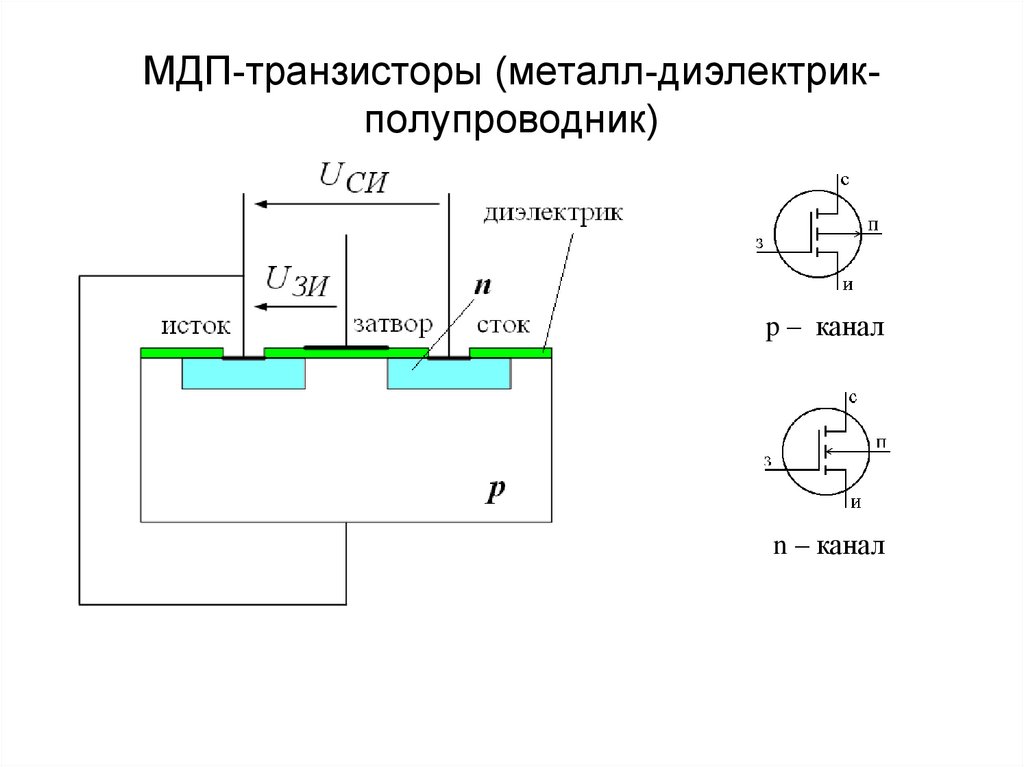

Формально, чтобы состояние S_t было марковским, вероятность того, что следующее состояние S_(t+1) будет s’, должна зависеть только от текущего состояния S_t = s_t , а не от остальных прошлых состояний S₁ = s₁ , S₂ = s₂ , … .

Подробнее о машинном обучении: как работает обратное распространение в нейронной сети?

Лекция о марковском процессе принятия решений с Дэвидом Сильвером. | Видео: Deep Mind

  

Объяснение марковского процесса

Вероятность перехода состояния. | Изображение: Rohan Jagtap

Марковский процесс определяется как (S, P) , где S — это состояния, а P — вероятность перехода состояния. Он состоит из последовательности случайных состояний S₁, S₂ , … , где все состояния подчиняются марковскому свойству.

Вероятность перехода в состояние или P_ss ’ — вероятность перехода в состояние с’ от текущего состояния с.

Образец цепи Маркова для примера робота. | Изображение: Rohan Jagtap

Чтобы понять концепцию, рассмотрим приведенный выше пример цепи Маркова. Сидеть, стоять, разбиться и т. д. — это состояния, и даны соответствующие им вероятности перехода из одного состояния в другое.

 

Марковский процесс вознаграждения (MRP)

Вероятность перехода состояния и вознаграждение в MRP. | Изображение: Rohan Jagtap

Марковский процесс вознаграждения (MRP) определяется (S, P, R, γ) , где S — состояния, P — вероятность перехода состояния, R_s — вознаграждение, а γ — коэффициент дисконтирования, который будет покрываться. в ближайших разделах.

Награда за состояние R_s является ожидаемой наградой по всем возможным состояниям, в которые можно перейти из состояния s .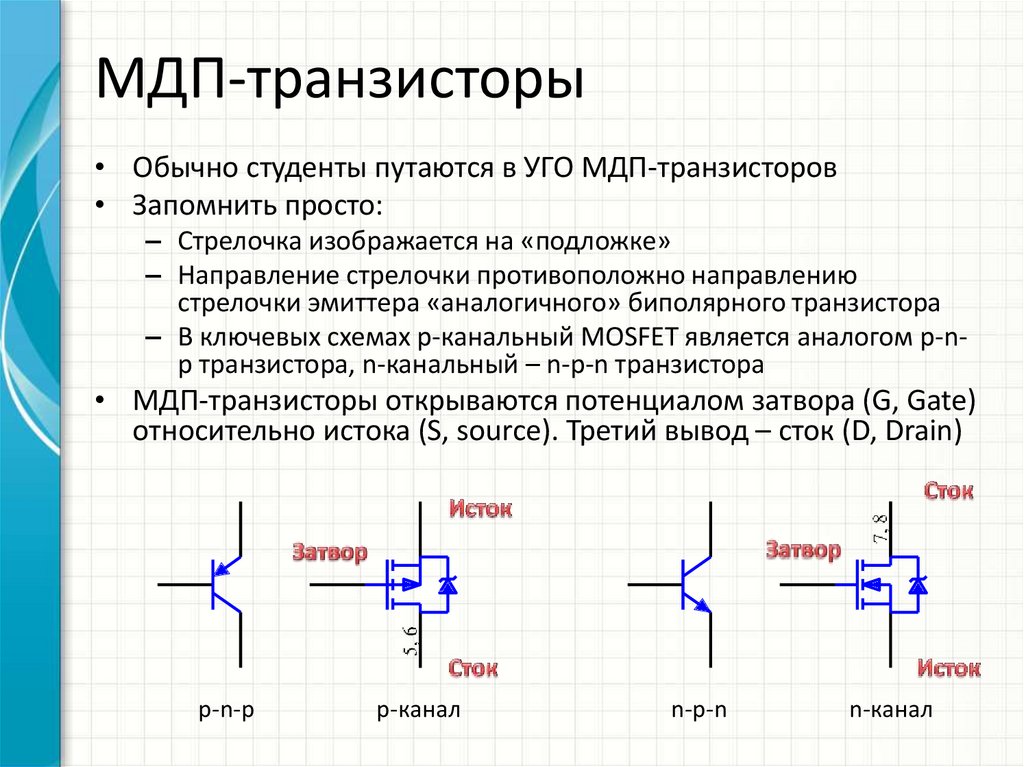 Эта награда получена за нахождение в состоянии S_t . По соглашению считается, что вознаграждение получено после того, как агент покинет состояние, и, следовательно, считается равным 9.0396 R_(t+1) .

Например:

Простой пример ППМ. | Изображение: Rohan Jagtap

 

Марковский процесс принятия решений (MDP)

Вероятность перехода состояния и вознаграждение в MDP | Изображение: Rohan Jagtap

Марковский процесс принятия решений (MDP) определяется (S, A, P, R, γ) , где A — набор действий. По сути это MRP с действиями. Введение в действия выявляет понятие контроля над марковским процессом. Раньше вероятность перехода состояния и вознаграждение за состояние были более или менее стохастическими (случайными). Однако теперь вознаграждение и следующее состояние также зависят от того, какое действие выберет агент. По сути, теперь агент может управлять своей судьбой (до некоторой степени)9. 0007

Теперь мы обсудим, как использовать MDP для решения проблем с RL.

 

Возврат (G_t)

Возврат уравнения G_t. | Изображение: Rohan Jagtap

Награды временные. Даже после выбора действия, дающего достойную награду, в долгосрочной перспективе мы можем упустить большую общую награду. Это долгосрочное общее вознаграждение и есть Возврат. Однако на практике мы рассматриваем Возвраты со скидкой.

 

Скидка (γ)

Переменная γ ∈ [0, 1] на рисунке является коэффициентом дисконтирования. Интуиция, стоящая за использованием скидки, заключается в том, что нет уверенности в будущих наградах. Хотя важно учитывать будущие вознаграждения для увеличения дохода, не менее важно ограничить вклад будущих вознаграждений в доход (поскольку вы не можете быть на 100 % уверены в будущем).0007

А еще потому, что пользоваться скидкой математически удобно.

 

Политика (π)

Уравнение политики. | Изображение: Rohan Jagtap

Как упоминалось ранее, политика определяет мысль, лежащую в основе принятия решения (выбор действия). Он определяет поведение агента RL.

Формально политика представляет собой распределение вероятностей по набору действий a при заданном текущем состоянии s . Дает вероятность выбора действия a в состоянии s .

Подробнее о машинном обучении: нейронные сети-трансформеры: пошаговое описание

 

Функции значений

Функция значения — это долгосрочное значение состояния или действия. Другими словами, это ожидаемый возврат по состоянию или действию. Это то, что мы действительно заинтересованы в оптимизации.

 

Функция значения состояния для MRP

Функция значения состояния для MRP. | Изображение: Рохан Джагтап

Функция значения состояния v(s) является ожидаемым возвратом, начиная с состояния с .

 

Уравнение ожидания Беллмана для марковского процесса вознаграждения (MRP)

Уравнение Беллмана дает стандартное представление для функций ценности. Он разбивает функцию стоимости на две составляющие:

1. Немедленное вознаграждение R_(t+1) .
2. Дисконтированная стоимость будущего состояния γ.v(S_(t+1)) .

Решение уравнения Беллмана для функции цены состояния. | Изображение: Rohan JagtapОбъяснение решения уравнения Беллмана. | Изображение: Rohan Jagtap

Давайте рассмотрим следующий сценарий (для простоты мы будем рассматривать только MRP):

Интуиция по уравнению Беллмана. | Изображение: Rohan Jagtap

Агент может переходить из текущего состояния s в некоторое состояние s ’ . Теперь функция значения состояния в основном представляет собой ожидаемое значение доходности по всем с ’ . Теперь, используя то же определение, мы можем рекурсивно заменить возврат следующего состояния s ’ функцией значения s ’ . Это именно то, что делает уравнение Беллмана:

Теперь давайте решим это уравнение:

Решение для функции цены. | Изображение: Rohan Jagtap

Поскольку ожидание является дистрибутивным, мы можем решить для обоих R_(t+1) и v(s’) отдельно. Мы уже видели, что математическое ожидание R_(t+1) свыше S_t=s является государственной наградой R_s . И математическое ожидание v(s’) по всем s’ берется по определению математического ожидания.

Другими словами, награда за состояние — это постоянная величина, которую мы так или иначе получим за то, что находимся в состоянии с . А другой член — это среднее значение состояния по всем 90 396 s’ 90 397.

 

Функция значения состояния для марковского процесса принятия решений (MDP)

Функция значения состояния для MDP. | Изображение: Rohan Jagtap

Это похоже на функцию стоимости для MRP, но есть небольшая разница, которую мы вскоре увидим.

 

Функция значения действия для марковского процесса принятия решений (MDP)

Функция значения действия для MDP. | Изображение: Рохан Джагтап

MDP вводят управление в MRP, рассматривая действия как параметр для перехода состояния. Значит, нужно оценивать действия наряду с состояниями. Для этого мы определяем функции ценности действия, которые дают нам ожидаемую отдачу от действий.

Функции значения состояния и функции значения действия тесно связаны. Мы увидим, как в следующем разделе.

 

Уравнение ожидания Беллмана (для MDP)

Уравнение ожидания Беллмана для MDP. | Изображение: Рохан Джагтап

Поскольку теперь мы знаем основы уравнения Беллмана, мы можем перейти к решению этого уравнения и посмотреть, чем оно отличается от уравнения Беллмана для MRP:

Интуиция по уравнению Беллмана. | Изображение: Rohan Jagtap

Мы представляем состояния с помощью кружков и действия с помощью точек; обе приведенные выше диаграммы представляют собой представление одного и того же MDP на разных уровнях. Левая половина изображения — это представление, ориентированное на состояние, а правая — представление, ориентированное на действие.

Давайте сначала разберемся с цифрой:

• Обведите точку: Агент находится в состоянии s ; он выбирает действие и в соответствии с политикой. Скажем, мы учим агента играть в шахматы. Один временной шаг эквивалентен одному полному ходу (один ход белых и один ход черных соответственно). В этой части перехода агент выбирает действие (делает ход). Агент полностью контролирует эту часть, когда он выбирает действие часть полностью контролируется агентом, поскольку он выбирает действие.
• Точка в кружке: Среда воздействует на агента и переводит его в состояние, основанное на вероятности перехода. Продолжая пример с агентом, играющим в шахматы, отметим, что это часть перехода, в которой противник делает ход. После обоих ходов мы называем это полным переходом состояния. Агент не может контролировать эту часть, поскольку он не может контролировать то, как действует среда, а только свое собственное поведение.

Теперь мы рассматриваем их как два отдельных мини-перехода:

Решение для функции значения состояния. | Изображение: Рохан Джагтап

Поскольку у нас есть переход от состояния к действию, мы берем ожидаемое значение действия для всех действий.

И это полностью удовлетворяет уравнению Беллмана, поскольку то же самое делается для функции ценности действия:

Решение для функции ценности действия. | Изображение: Rohan Jagtap

Мы можем подставить это уравнение в функцию значения состояния, чтобы получить значение с точки зрения рекурсивных функций значения состояния (и наоборот), подобных MRP:

Подстановка функции значения действия в функцию значения состояния и наоборот. | Изображение: Рохан Джагтап

 

Марковский процесс принятия решений Функции оптимального значения

Представьте, что если бы мы получили значение для всех состояний/действий MDP для всех возможных шаблонов действий, которые можно выбрать, то мы могли бы просто выбрать политику с наибольшим значением для состояния и действия. Уравнения выше представляют именно это. Если мы получим q∗(s, a) , то задача решена.

Мы можем просто присвоить вероятность 1 действию, имеющему максимальное значение для q∗ и 0 для остальных действий для всех заданных состояний.

Оптимальная политика. | Изображение: Rohan Jagtap

 

Уравнение оптимальности Беллмана

Уравнение оптимальности Беллмана для оптимальной функции значения состояния. | Изображение: Rohan Jagtap

Поскольку мы все равно собираемся выбрать действие, которое дает max q∗ , мы можем назначить это значение в качестве функции оптимального значения.