Логическое мышление: Урок 2. Понятие в логике

Содержание

Урок 2. Понятие в логике

Скорее всего, немногие люди задумываются над тем, что они мыслят и рассуждают с помощью понятий. Понятия подобны воздуху: мы их не замечаем, но при этом не можем без них размышлять. Каждый ребёнок естественно научается думать с их помощью в семь-восемь лет, переходя от оперирования с конкретными предметами к оперированию с идеями. Тем не менее, это не означает, что каждый умеет правильно ими пользоваться, а ведь без этого умения путь к логичному рассуждению закрыт. Вот почему в этом уроке, мы расскажем, что такое понятия, какие бывают виды понятий, как разные понятия соотносятся друг с другом и как с ними правильно обращаться.

Содержание

Что такое понятие?
Виды понятий
Отношения между понятиями
Операции над понятиями
Упражнения
Проверочные вопросы на усвоение материала

Что такое понятие?

Что такое понятие? Вроде бы интуитивно ясно.

Возможно, многие скажут: понятие – это то же, что и слово или термин. Однако такое определение неверно. Понятия выражаются словами и терминами, но не идентичны им. Напомним, в прошлом уроке мы говорили, что все слова нашего языка – это знаки, обладающие двумя характеристиками: значением и смыслом. Обычно мы пользуемся языком интуитивно, не задумываясь о значении и смысле. Мы просто называем одни объекты яблоками, другие грушами, третьи апельсинами. Часто мы выбираем то или иное слово, руководствуясь контекстом, то есть границы его употребления размыты. Между тем, нередки ситуации, когда такое интуитивное употребление слов неприемлемо или приводит к неприятным последствиям. Представьте, например, что вы всей семьей собираетесь на отдых заграницу. Вы подаёте вместе документы на визу, и для этого вам нужно, чтобы ваш супруг (или ваша супруга) взял на работе справку о зарплате. Вы говорите ему: «Не забудь взять необходимую бумагу». Вечером он приносит вам пачку прекрасной бумаги А4. В данной ситуации каждый из вас понял слово «бумага» по-своему, и это стало причиной обоюдного непонимания.

Во многих сферах (законодательство, судопроизводство, должностные и технические инструкции, наука и т.п.) подобная двусмысленность должна быть исключена. Бороться с ней как раз и призваны понятия.

С точки зрения логики, понимать слово означает быть в состоянии указать, какие именно предметы им обозначаются, то есть уметь устанавливать относительно любого предмета, можно ли его назвать данным словом или нет. Каким образом этого достичь? Через образование понятия.

Понятие – это логическая мыслительная операция, которая по определённым признакам выделяет предметы из множества и объединяет их в один класс.

Таким образом, в образовании понятия участвуют три компонента: слово или словосочетание (знак), совокупность объектов, которые им обозначаются (значение), и некоторая идея или отличительный признак, связывающий данное слово с подпадающими под него объектами (смысл). Именно этот отличительный признак выступает сердцем понятия, потому что он связывает слово и объекты.

В качестве примера можно привести понятие квадрата. «Квадрат» – это термин, отличительный признак – «правильный четырёхугольник, у которого равны все углы и стороны», объекты – множество геометрических фигур, обладающих этим признаком. Что делает понятие квадрата? Из всего множества геометрических фигур оно выделяет какую-то группу фигур, потому что они обладают набором каких-то особых признаков.

Важно не путать понятие и слово, которым оно обозначается. Иногда с одним словом могут связываться разные понятия в зависимости от того, что берётся в качестве отличительного признака. Например, со словом «человек» могут связываться следующие понятия: «существо социальное», «существо, обладающее разумом», «существо, способное создавать орудия», «существо, обладающее членораздельной речью» и т.д. Однако нужно учитывать, что для краткости люди чаще всего говорят просто о понятии квадрата или понятии человека, не уточняя, какой именно отличительный признак ложится в основу выделения этого понятия.

Это часто приводит к разногласиям и так называемым спорам о словах. Поэтому прежде чем вступать в спор, полезно уточнить, какое именно понятие ваш собеседник вкладывает в то или иное слово.

Виды понятий

Каждое понятие обладает двумя характеристиками: содержанием и объёмом. Содержание понятия – это та совокупность отличительных признаков, на основании которой предметы выделяются из универсума и обобщаются в одну группу. Объём понятия

– это совокупность всех предметов, которые обладают отличительными признаками. Важно отметить, что объём понятия всегда задаётся относительно некоторого универсума рассмотрения, то есть множества объектов, которые в принципе могут обладать теми или иными отличительными признаками. Универсумом рассмотрения могут быть люди, живые существа, числа, химические соединения, бытовые приборы, науки, пищевые продукты и т.д. Так понятие «слоны» задаётся на универсуме живых существ, понятие «физика» – на универсуме наук, понятие «чётные числа» – на универсуме чисел, понятие «сыр» – на универсуме пищевых продуктов.

Содержание и объём понятия ложатся в основу разделения понятий на разные виды.

В зависимости от объёма понятия делятся на пустые и непустые. В объёме пустых понятий не содержится ни одного элемента. В объёме непустых понятий есть хотя бы один элемент. Если элемент всего один, то речь идёт о единичном понятии (автор «Войны и мира»), если их много – то об общих понятиях («французские короли»). Если объём понятия совпадает с универсумом рассмотрения, то говорят об универсальных понятиях («числа», «люди»)

Поговорим подробнее о пустых понятиях. Мы не всегда это замечаем, но пустые понятия используются людьми довольно часто. Это может происходить неосознанно, но иногда с их помощью нас стараются ввести в заблуждение. С одним примером пустого понятия мы уже сталкивались в прошлом уроке: «нынешний король Франции». Во всём универсуме людей нет ни одного человека, который обладал бы отличительным признаком «быть нынешним королём Франции». Нужно отметить, что в данном случае понятие оказалось пустым в силу исторического стечения обстоятельств. Пойди история по-другому, это понятие могло бы быть непустым. Другой пример пустого понятия – «вечный двигатель». Здесь пустота обусловлена не историческими причинами, а законами природы. Что касается научных понятий, то относительно многих из них неизвестно, пустые они или нет. Хорошей иллюстрацией этому служит понятие «бозон Хиггса», непустота которого подтвердилась лишь недавно с открытием новой частицы, удовлетворяющей отличительным признакам этого понятия. Понятие может быть пустым и в силу законов логики. Это так называемые самопротиворечивые понятия, к примеру, «круглый квадрат».

В зависимости от типов обобщаемых предметов понятия делят на собирательные и несобирательные, абстрактные и конкретные. К собирательным понятиям относятся понятия о множествах предметов или людей. Такие понятия обычно содержат следующие термины: «множество», «класс», «совокупность», «группа», «стая» и т.п. Примеры собирательных понятий: «рабочий коллектив завода», «рок-группа», «созвездие».

Несобирательные понятия относятся к единичным предметам: «компьютер», «дерево», «звезда».

Конкретными считаются понятия, элементами объёма которых являются индивиды или совокупности индивидов. Важно отметить, что под индивидами здесь понимаются не люди, а индивидуальные объекты, причём даже если эти объекты являются абстрактными сущностями. Поэтому примером конкретного понятия может быть «Солнечная система», «натуральные числа». К числу абстрактных понятий относят понятия, элементами объёма которых являются свойства, предметно-функциональные характеристики, отношения, например: «красота», «твёрдость».

По типу содержания понятия делятся на положительные и отрицательные, относительные и безотносительные. Отрицательные понятия содержат знак логического отрицания, положительные понятия, соответственно, не содержат его. Все примеры понятий, которые мы приводили, были положительными. Пример отрицательного понятия: «нечётные числа». Относительные понятия в качестве отличительного признака подпадающих под него объектов берут так называемые реляционные свойства, то есть свойства, образованные от некоторого отношения.

Примером относительного понятия будет человек как «существо, способное производить орудия труда». Среди относительных понятий можно выделить пары взаимосвязанных понятий, предполагающих друг друга: «учитель» и «ученик», «продавец» и «покупатель». Безотносительными называются понятия о предметах, отличительным признаком которых не является реляционное свойство, например: «цитрусовые фрукты».

Вся эта довольно сложная типология понятий нужна для того, чтобы мы могли с лёгкостью производить над понятиями операции и определять в каких отношениях друг к другу они находятся.

Отношения между понятиями

Понятия не изолированы друг от друга, наоборот, они находятся во множестве связей с другими понятиями. Умение выявлять эти связи очень важно, так как оно позволяет выявить, когда наш собеседник или автор текста ошибается в употреблении понятий или даже осознанно ими манипулирует. Примерами такой манипуляции могут послужить использование понятий, объёмы которых не равны, как взаимозаменяемых, незаметный переход к понятию с меньшим объёмом для облегчения доказательства своей позиции и т.

д.

Прежде чем выяснять, в каком отношении находятся два понятия, нужно определить, сравнимы ли они вообще или нет. Грубо говоря, понятие «собаки» и понятие «натуральные числа» ни в каком отношении находиться не могут, потому что они отсылают к разным универсумам рассмотрения: в первом случае животных, а втором – чисел. Хотя если, например, наш универсум рассмотрения – это вещи, которыми интересуются люди, то эти два понятия становятся сравнимы, так как люди интересуются и тем, и другим. Таким образом, прежде чем сравнивать понятия, нужно убедиться, что они, фигурально выражаясь, имеют один знаменатель – отсылают к одному универсуму.

Логики делят отношения между понятиями на фундаментальные и производные. Фундаментальные отношения первичны, с помощью их различных комбинаций можно задать все остальные отношения. Всего выделяют три фундаментальных отношения: совместимость, включение и исчерпывание.

Понятия совместимы, если пересечение их объёмов непусто. Соответственно, если пересечение их объёмов пусто, то понятия несовместимы.

Понятие А включается в понятие В, если каждый элемент объёма А также является элементом объёма В.

Понятия находятся в отношении исчерпывания, если и только если каждый предмет из универсума рассмотрения является элементом объема либо первого, либо второго понятия.

В результате комбинирования этих фундаментальных отношений можно задать пятнадцать производных отношений между понятиями. Мы расскажем только о тех из них, которые оперируют с непустыми и неуниверсальными понятиями. Их всего шесть.

Равнообъёмность – это отношение, при котором объёмы двух понятий полностью совпадают.

При равнообъёмности понятия А и В живут в одном кружочке. Примером может служить пара понятий: «треугольник с равными сторонами» и «треугольник с равными углами». Оба этих понятия обозначают одну и ту же совокупность объектов.

Подчинение возникает тогда, когда объём одного понятия полностью входит в объём другого понятия.

Кружочек В полностью располагается в кружочке А, и при этом кружочек А больше чем В по объёму, то есть в А входят объекты, которые не входят в В. Иллюстрация подчинения – отношения между понятиями «цитрусовые фрукты» (А) и «апельсины» (В).

Пересечение – это отношение, при котором объёмы понятий пересекаются, но полностью не совпадают.

Пример пересечения – отношение между понятиями «женщины» и «руководители». Существуют люди, которые обладают и первой, и второй характеристикой.

Дополнительность – это такое отношение, когда два понятия пересекаются и при этом исчерпывают собой весь универсум рассмотрения.

Я специально изобразила понятия А и В разными цветами, чтобы было видно, что кружок в центре – это не отдельное понятие, а результат их пересечения. Отношение дополнительности существует, например, между понятиями «температура выше 0°С» и «температура ниже 30°С». Объёмы этих понятий пересекаются, и при этом объём их сложения равен объёму универсума рассмотрения.

Противоречие – это отношение, при котором объёмы понятий не пересекаются и исчерпывают весь универсум.

Если, к примеру, универсум рассмотрения – это люди, то А может быть понятием «работающие», а В – «безработные». Каждый человек может быть либо работающим, либо безработным, но не ими вместе и не чем-то третьим.

Соподчинение возникает, когда объёмы понятий не пересекаются, но при этом не исчерпывают собой весь универсум рассмотрения.

Сразу скажу, что я не знаю, чем руководствовались те, кто назвал это отношение соподчинением. На мой взгляд, речь скорее идёт о независимости друг от друга. Видимо, имеется в виду, что оба понятия находятся в отношении подчинения к какому-то третьему понятию – в данном случае всему универсуму рассмотрения. Предположим, что универсум рассмотрения – это животные. Тогда понятие А – «ящерицы», понятие В – «кошки». И ящерицы, и кошки – это животные. Объёмы этих понятий не пересекаются. При этом объём универсального понятия «животные» содержит множество не подпадающих под А и В элементов.

Закон обратного отношения между содержанием и объёмом понятия

В самом начале мы сказали, что понятие обладает двумя характеристиками: содержанием и объёмом. Соответственно, когда мы определяем отношение между понятиями, имеют значение не только их объёмные характеристики, но и содержательные. В частности, логики выяснили, что между объёмом и содержанием понятий существует так называемый закон обратного отношения. Суть этого закона состоит в следующем: если первое понятие ýже по объёму, чем второе понятие, то тогда первое понятие богаче второго по содержанию. По большому счёту, этот закон действует, когда мы сталкиваемся с отношением подчинения между понятиями. Предположим, первое понятие – это «цветы», второе понятие – это «ромашки». Понятие «ромашки» ýже по объёму, чем понятие «цветы», то есть в него входит меньше элементов. Зато оно богаче по содержанию. Это означает, что из понятия «ромашки» мы можем извлечь больше информации, чем из понятия «цветы». Если некий объект подпадает под понятие «ромашка», то мы автоматически знаем, что он также будет подпадать под понятие «цветы», а вот заключение в обратную сторону сделать нельзя. Если некий объект является элементом понятия «цветы», то это совсем не значит, что он также будет элементом понятия «ромашка». Он вполне может быть пионом, розой, лавандой и т.д.

Операции над понятиями

Главная цель операций над понятиями – образование нового понятия, со своим собственным объёмом и содержанием, из имеющихся других или более понятий. Основные операции, совершаемые над понятиями, называются булевыми операциями. Такое наименование они получили в честь английского математика и логика Дж. Буля, который разработал своеобразную логическую математику. Правда, операции, совершаемые над понятиями, похожи на те операции, которые мы научились выполнять с числами в начальной школе. К ним относятся: пересечение, объединение, вычитание, симметрическая разность, дополнение.

Пересечение понятий – это операция, в ходе которой берутся два или более понятий и как бы накладываются друг на друга. В результате в месте пересечения их объёмов образуется новое понятие, элементами которого будут те предметы, которые одновременно обладают отличительными признаками всех пересечённых понятий. Чтобы представить это наглядно, посмотрим на рисунки:

Результат пересечения – заштрихованная область. Например, если мы возьмём понятие «полицейские» и понятие «коррупционеры» и произведём над ними операцию пересечения, то в заштрихованной области окажутся только те люди, которые одновременно являются и полицейскими и коррупционерами. Так мы образовали новое понятие «полицейские-коррупционеры». Как видно, операция пересечения базируется на отношении пересечения. Это означает, что, если два понятия находятся в отношении пересечения, то мы легко можем образовать с их помощью новое понятие.

Объединение понятий подобно сложению: мы берём несколько понятий, соединяем их объёмы и тем самым образуем новое понятие, элементами которого будут те предметы, которые обладают хотя бы одним из отличительных признаков объединённых понятий.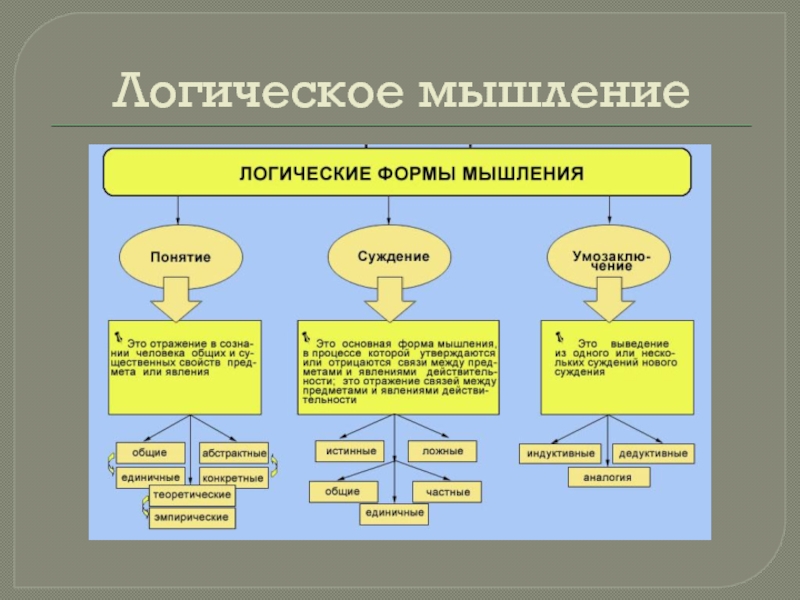

Для иллюстрации мы можем взять понятия «курильщики» и «люди, употребляющие алкоголь» и посредством объединения образовать понятие «люди, которые курят или употребляют алкоголь». В данном случае под понятие будут подпадать не только те люди, которые одновременно и курят, и пьют, но все те, кто обладает хотя бы одной из этих вредных привычек. Поэтому мы заштриховали оба кружочка.

Вычитание понятий опять же очень похоже на математическое вычитание. При вычитании берётся два или более понятий и из объёма одного отнимаются объёмы оставшихся. Таким образом, образуется новое понятие, элементами объёма которого будут предметы, обладающие отличительным признаком первого понятия, но не обладающие отличительными признаками тех понятий, которые из него вычитались.

Предположим, что понятие А – это «люди, страдающие диабетом», понятие В – «люди, страдающие избыточным весом». Если мы вычитаем понятие В из понятия А, то мы получаем новое понятие «люди, страдающие диабетом, но не имеющие избыточного веса». Оно показано заштрихованной областью.

Симметрическая разность – это операция, в некотором смысле обратная пересечению. Нужно точно также взять два или более понятий, наложить их друг на друга, но новое понятие, образованное в результате этого наложения, будет содержать только те элементы, которые обладают не более чем одним отличительным признаком изначальных понятий.

Заштрихованная область показывает это новое понятие. Предметы, подпадающие под это понятие должны обладать признаком А или В, но не ими вместе. Пусть А – это понятие «врач», В – «мужчина». Тогда получаем следующее понятие: «быть врачом, но не быть мужчиной, либо быть мужчиной, но не быть врачом».

Дополнение – это операция, в ходе которой берётся понятие, а затем его объём как бы вычитается из всего универсума рассмотрения. Так создаётся новое понятие, элементами которого будут только те предметы, которые не обладают отличительным признаком изначально взятого понятия.

Новое понятие А’ – дополнение к понятию А. Если универсум нашего рассмотрения – это животные, понятие А – «млекопитающие», то А’ – «животные, не являющиеся млекопитающими». Операцию дополнения не нужно путать с отношением дополнительности.

Помимо булевых операций над понятиями можно проводить ещё целый ряд операций: ограничение, обобщение, деление.

Ограничение – это операция, представляющая собой как бы сужение понятия. Ограничить понятие А означает перейти к понятию В, такому что его объём будет строго включаться в объём понятия А. Причём этот переход от А к В представляет собой переход от родового понятия к видовому.

Как видно из картинки, в результате ограничения кружочек, представляющий объём понятия, становится меньше. Мы ограничиваем понятие А до понятия В, а затем – понятие В до понятия С. Можно предположить, что понятие А – это «рыбы». Мы можем ограничить его до понятия В – «акулы». Объём понятия А шире, так как рыбы бывают разные, они включают много видов – не только акул. При этом объём понятия В полностью включается в объём понятия А, потому что все акулы – это рыбы. Понятие «акулы» можно ограничить до понятия С – «белые акулы». Опять же понятие «белые акулы» полностью входит в понятие «акулы», но меньше его по объёму. Пределом ограничения понятия выступает единичное понятие. На нашем рисунке оно представляло бы точку в центре, которую уже нельзя сузить.

Операция ограничения понятий нередко сопровождается ошибками. Чаще всего они связаны с тем, что ограничение понятий путают с членением предметов, то есть понятие ограничивают не на основании родовидовых признаков, а на основании тех частей, на которые разделяются элементы их объёмов. Например, возьмём понятие «автомобили». По родовидовым признакам мы можем ограничить его до понятий «автомобили с ручной коробкой передач» или «электромобили». И это правильное ограничение. Однако автомобиль состоит из множества компонентов: фары, колёса, руль, дворники, двигатель и т.д. Поэтому можно встретить такой вариант: понятие А – «автомобили» ограничивают до понятия В – «колёса». Хотя колёса – это часть автомобиля, такое ограничение неверно. Существует лёгкий способ избежать этой ошибки. При правильном ограничении понятия А до понятия В, должно быть верным высказывание «Все В есть А»: «Все акулы – это рыбы», «Все электромобили – это автомобили». Если мы применяем эту формулу к автомобилям и колёсами, получается: «Все колёса – это автомобили». Высказывание неверно, значит, операция ограничения была проведена неправильно.

Обобщение – это операция, обратная ограничению. На этот раз мы не сужаем, а расширяем понятие. Обобщить понятие В означает перейти к понятию А, так что объём понятия В будет строго включаться в объём понятия А. Здесь совершается переход от видового понятия к родовому.

Понятие С, представленное самым маленьким кружочком, мы обобщаем до понятия В, которое в свою очередь мы можем ещё обобщить до понятия А, причём С полностью включается в В, и В полностью включается в А. Пусть С – это понятие «золото», тогда мы можем обобщить его до понятия В – «металлы», а понятие В – до понятия А – «химические элементы». Предел обобщения – это универсальное понятие, то есть понятие, объём которого совпадает с универсумом рассмотрения. В нашем примере понятие «химические элементы» как раз может быть рассмотрено как универсальное.

Операция обобщения понятий может быть подвержена той же самой ошибке, что и ограничение: часто люди обобщают понятия на основании не родовидовых признаков, а составных частей. В частности, понятие «крылья» обобщают до понятия «птицы», что неверно. Способ проверки тот же самый: посмотреть правильным ли будет утверждение «Все В есть А». Очевидно, что утверждение «Все крылья – это птицы» некорректно.

Деление – это операция, состоящая в том, что берётся понятие, выделяется какая-то характеристика и на основе варьирования этой характеристики исходное понятие делится на несколько частей, в результате чего получается набор новых понятий. Исходное понятие называют делимым понятием. Те понятия, которые образуются после деления – членами деления. Характеристику, на основе которой осуществляется деление – основанием деления.

Весь кружочек – это объём понятия делимого понятия А. В, С, D и Е – члены деления, то есть понятия, образованные в результате деления понятия А. Для иллюстрации предположим, что понятие А – это «месяцы». Основание деления – это принадлежность к времени года. Тогда новообразовавшиеся понятия В, С, D и Е – это «зимние месяцы», «весенние месяцы», «летние месяцы» и «осенние месяцы». Очевидно, что в результате деления может получаться разное количество понятий: всё зависит от делимого понятия и основания деления.

Чтобы деление было правильным, необходимо соблюдать следующие условия:

Деление должно производиться только по одному основанию. Если использовать наш пример с понятием месяцы, то я не могу разделить его на следующие подпонятия: «зимние месяцы», «весенние месяцы», «летние месяцы», «осенние месяцы» и «мои любимые месяцы». В таком делении используются две характеристики: принадлежность к времени года и моё отношение к конкретному месяцу. Это называется путанным делением. Также если использовать больше, чем одно основание деления, можно совершить так называемый скачок в делении, состоящий в том, что одни члены деления являются видами А, а другие – его подвидами. Например, исходное понятие – «вино», основание деления – цвет. В результате правильного деления мы должны получить три новых понятия: «белое вино», «розовое вино» и «красное вино». Но если в делении совершён скачок, то можно прийти к такому результату: «белое вино», «розовое вино», «каберне», «шираз», «мерло», «пино нуар». В данном случае были совмещены два основания: цвет и сорт, и в члены деления одновременно попали виды вида (белое, розовое) и подвиды (каберне, шираз и т.д.).
Члены деления В, С и т.д. должны представлять собой виды по отношению к родовому понятию А. Это то же условие, с которым мы сталкивались при ограничении и обобщении. Нельзя разделить понятие «автомобиль» на понятия «колёса», «двигатель», «руль» и т.п. Опять же нужно задаться вопросом, верно ли утверждение «Все В есть А», «Все С есть А» и так по всем членам деления. Если же вас всё-таки интересуют колёса и двигатель, то необходимо заменить делимое понятие на «части автомобиля», тогда деление станет правильным.
Объёмы членов деления не пересекаются, то есть ни один из элементов не может одновременно попадать в В и С или в В и Е и т.д.
Члены деления не могут быть пустыми понятиями. Предположим, что исходное понятие А – это «ныне правящие короли». Основание деления – принадлежность к странам. Так вот, среди членов деления не может быть понятий «ныне правящие французские короли» или «ныне правящие немецкие короли», так как это пустые понятия.
Если над всеми членами деления B, C, D, E произвести операцию объединения, то мы должны получить объём делимого понятия A.

Существует два вида деления: дихотомическое деление и деление по видоизменению основания. Слово «дихотомический» дословно переводится с греческого как «деление надвое». При его осуществлении исходное понятие делится всего лишь на два новых понятия. Выбирается какое-либо основание деления, то есть признак, и в зависимости от наличия или отсутствия этого признака все элементы объёма разделяются на две части. Пусть делимым понятием будет понятие «люди», основанием деления – наличие высшего образования. В таком случае наше исходное понятие будет разделено на два: «люди, имеющее высшее образование» и «люди, не имеющие высшего образования». Другой пример: возьмём понятие «собаки», основание деления – породистость. В результате дихотомического деления получаем понятия: «породистые собаки», «беспородные собаки».

Второй вид деления – деление по видоизменению основания. В его результате мы можем получить более двух новых понятий. Здесь в качестве основания выбирается какая-либо предметно-функциональная характеристика элементов объёма исходного понятия. В нашем примере с месяцами такой характеристикой была принадлежность к времени года. Если наше делимое понятие – это «люди», то можно в качестве основания деления взять цвет глаз, цвет волос, национальность и т. п. Если делимое понятие – «стихотворения», то основанием деления может быть их жанровая принадлежность. Для иллюстрации возьмём понятие «игральные карты», а основанием деления сделаем масть:

Классификация. Операция деления лежит в основе составления классификаций и типологий. Классификация осуществляется посредством последовательного деления понятия на его виды, видов – на подвиды и т.д. Классификация, прежде всего, важна в научном познании. Она может выступать как результатом изучения какой-то предметной области (всеобщая классификация растений и животных Карла Линнея), так и двигателем исследований (периодическая таблица химических элементов Менделеева). Кроме того, классификации очень важны в обучении: люди гораздо легче воспринимают информацию, если она разложена по полочкам. Часто даже сами того не замечая, мы пользуемся классификациями и в повседневной жизни: ранжирование сотрудников в офисе, организация одежды в шкафу, распределение товаров по отделам в магазине – вот только несколько примеров.

Правильно выполненная классификация подобна перевёрнутому дереву (на мой взгляд, скорее, перевёрнутому кусту). Вершина классификации – исходное делимое понятие – называется корнем. Линии, расходящиеся от неё, подобны веткам. Они ведут к членам деления, от которых в свою очередь также расходятся ветки к новым понятиям. Каждое понятие в классификации называют таксоном. Таксоны группируются по ярусам. На первом ярусе находится корень классификации А. На втором ярусе – таксоны В₁-В_n, образованные с помощью первой операции деления. На третьем ярусе – таксоны С₁-С_n, образованные в результате второй операции деления и т.д. Каждый ярус может содержать любое количество таксонов.

При построении классификаций используются оба вида деления: и дихотомическое, и по видоизменению основания. При этом они могут соседствовать даже в одной классификации. Дело в том, что внутри классификации каждая отдельная операция деления может производиться по своему собственному основанию. Приведём пример. Возьмём в качестве корня классификации понятие «писатели», основание деления – являлся ли писатель русским или нет. Соответственно, производим дихотомическое деление, в результате которого получаем на втором уровне два новых понятия: «русские писатели» и «зарубежные писатели». Затем мы можем разделить понятие «русские писатели» по видоизменению основания. В качестве основания возьмём характеристику: «в каком веке жил писатель?» Получаем новые понятия: «русские писатели XIвека», «русские писатели XIIвека» и так вплоть до «русских писателей XXIвека». Что касается понятия «зарубежные писатели», то его тоже можно разделить по видоизменению основания, но в качестве основания взять национальность писателей. Таким образом, получим: «испанские писатели», «французские писатели», «немецкие писатели» и т.д.

Знаком […] обозначены пропущенные члены деления. Дальше каждый таксон может быть разделён ещё по какому-то своему признаку. Главное в каждом отдельном делении соблюдать перечисленные выше правила.

Нужно отметить, что составление классификаций – не такая простая задача, как может показаться на первый взгляд. Не редки ситуации, когда сложно или невозможно определить, к какому именно таксону нужно относить тот или иной предмет. В нашем примере с писателями, в частности, возможны случаи, когда писатель родился и начал творить в одном веке, а умер уже в другом, как Чехов. Куда его нужно относить – в писатели XIXвека или XXвека? Иногда встречаются объекты, которые в принципе никуда не укладываются. Тогда для них создают отдельный таксон или помещают их в так называемый «отстойник». Он может обозначаться словами «всё прочее», и объекты, находящиеся в нём, не связаны ничем иным, кроме того, что их не удаётся никуда определить.

Упражнения

Китайская энциклопедия

Борхес в одном из своих произведений приводит отрывок из таинственной китайской энциклопедии. Это «божественное хранилище благотворных знаний» говорит, что «животные подразделяются на: а) принадлежащих Императору, б) бальзамированных, в) прирученных, г) молочных поросят, д) сирен, е) сказочных, ж) бродячих собак, з) включенных в настоящую классификацию, и) буйствующих, как в безумии, к) неисчислимых, л) нарисованных очень тонкой кисточкой из верблюжьей шерсти, м) и прочих, п) только что разбивших кувшин, о) издалека кажущихся мухами» (Борхес Х. Л. Аналитический язык Джона Уилкинса // Соч. в 3 т. Т. 2. Рига: Полярис, 1997, с. 85).

Попробуйте представить эту классификацию животных в виде дерева. Считаете ли вы, что она выполнена правильно? Если да, то докажите, что ни одно из правил деления в ней не нарушено. Если нет, то объясните, какие именно правила нарушены. Каким образом эту классификацию можно было бы исправить?

Мясо не еда

Кот. Прости, пожалуйста, за нескромность. Я тебя давно вот о чем хотел спросить…

Осел. Ну?

Кот. Как можешь ты есть колючки?

Осел. А что?

Кот. В траве попадаются, правда, съедобные стебельки. А колючки… сухие такие!

Осел. Ничего. Люблю острое.

Кот. А мясо?

Осел. Что – мясо?

Кот. Не пробовал есть?

Осел. Мясо – это не еда. Мясо – это поклажа. Его в тележку кладут, дурачок. (Е. Шварц, «Дракон»)

Определите отношения между понятиями «еда», «острые предметы», «острая еда», «колючки», «мясо» и «поклажа». Изобразите эти отношения с помощью графических схем. Помните, что понятия могут быть сравнимы, только если они принадлежат к одному универсуму рассмотрения.

Разговор мужа с женой

Муж: Милая, ты не права.

Жена: Ах, я не права. Значит, я лгу. Я лгу, значит, я плохой человек, то есть нелюдь. Ты хочешь сказать, что я животное? Мама, он меня скотиной назвал!

Определите, правильно ли был выполнен переход между понятиями «человек, который не прав», «лжец», «плохой человек», «нелюдь», «животное», «скотина». Обоснуйте свою позицию. Какие операции над понятиями использовались при этом переходе? В каких отношениях находятся эти понятия? Изобразите их с помощью графических схем.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Ксения Галанина

Урок 7. Силлогизмы

Этот урок будет посвящён многопосылочным умозаключениям. Так же как и в случае однопосылочных умозаключений, вся необходимая информация в скрытом виде будет присутствовать уже в посылках. Однако, поскольку посылок теперь будет много, то способы её извлечения становятся более сложными, а потому и добытая в заключении информация не будет казаться тривиальной. Кроме того, нужно отметить, что существует много разных видов многопосылочных умозаключений. Мы с вами сосредоточимся только на силлогизмах. Они отличаются тем, что и в посылках и в заключении имеют категорические атрибутивные высказывания и на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств.

Содержание:

Простой категорический силлогизм

Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С.

Приведём пример:

Все рыбы не могут жить без воды.
Все акулы – это рыбы.
Следовательно, все акулы не могут жить без воды.

В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»).

Естественно, в рассуждении посылки могут находиться в любой последовательности. Однако для удобства проверки правильности силлогизмов, большую посылку ставят всегда первой, а меньшую – второй. Тогда в зависимости от расположения терминов все простые категорические силлогизмы можно разделить на четыре вида. Эти виды называются фигурами.

Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина.

Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин.

Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например:

Всякий М есть P
Всякий S есть М
Всякий S есть P

или:

Ни один М не есть P
Некоторые М есть S
Некоторые S не есть P

Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить.

Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:

Фигура I

Фигура II

Фигура III

Фигура IV

Barbara (aaa)

Celarent (eae)

Darii (aii)

Ferio (eio)

Barbari (aai)

Celaront (eao)

Baroko (aoo)

Cesare (eae)

Camestres (aee)

Festino (eio)

Camestrop (aeo)

Cesaro (eao)

Bocardo (oao)

Disamis (iai)

Datisi (aii)

Ferison (eio)

Darapti (aai)

Felapton (eao)

Camenos (aeo)

Dimaris (iai)

Camenes (aee)

Fresison (eio)

Bramantip (aai)

Fesapo (eao)

К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так:

Ни один P не есть М
Все S есть М
Ни один S не есть P

Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M.

Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем.

Всякий P есть М
Всякий М есть S
Некоторые S есть P

Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:

Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным.

Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен.

Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным.

Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям:

Правила терминов

Простой категорический силлогизм должен включать только три термина.
Средний термин должен быть распределён хотя бы в одной из посылок.
Если больший или меньший термин не распределён в посылке, то он должен быть нераспределён и в заключении.

Правила посылок:

Хотя бы одна из посылок должна быть утвердительной.
Если обе посылки являются утвердительными, то и заключение должно быть утвердительным.
Если одна из посылок отрицательная, то и заключение должно быть отрицательным.

Правила посылок понятны, а правила терминов требуют некоторых пояснений. Начнём с правила о трёх терминах. Хотя оно кажется очевидным, оно довольно часто нарушается вследствие так называемой подмены терминов. Посмотрите на следующий силлогизм:

Золото – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.
Молчание – золото.
Молчание – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.

Прежде всего, если вы помните фигуры и правильные модусы, вы сразу можете сказать, что этот силлогизм неправильный, так как он относится ко второй фигуре и имеет модус aaa, который не принадлежит к списку правильных модусов для этой фигуры. Но если вы их не помните, всё равно вы можете выявить его ложность, потому что здесь явно присутствует четыре термина, вместо трёх. Термин «золото» употребляется в двух совершенно различных смыслах: как химический элемент и как нечто, обладающее ценностью. Посмотрим на более сложный пример:

Все книги из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь.
«Отцы и дети» Ивана Тургенева – книга из собрания Российской государственной библиотеки.
«Отцы и дети» Ивана Тургенева нельзя прочитать за целую жизнь.

Кажется, что этот силлогизм соответствует модусу Barbara первой фигуры. Однако посылки истинны, а заключение ложно. Проблема в том, что в этом примере опять произошло учетверение терминов. Вроде бы этот силлогизм содержит три термина. Меньший термин – «”Отцы и дети” Ивана Тургенева». Больший термин – «книги, которые нельзя прочитать за целую жизнь». Средний термин – «книги из собрания Российской государственной библиотеки». Если же присмотреться внимательно, то станет ясно, что субъектом первой посылки является не термин «книги из собрания Российской государственной библиотеки», а термин «все книги из собрания Российской государственной библиотеки». В данном случае «все» – это не квантор общности, а часть субъекта, так как это слово употребляется не в разделительном смысле (каждый в отдельности), а в собирательном (все вместе). Если бы мы заменили слово «все» на слова «каждый в отдельности», то первая посылка попросту стала бы ложной: «Каждую в отдельности книгу из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь». Таким образом, мы получаем четыре термина вместо трёх, а потому это умозаключение ложно.

Теперь перейдём к правилам о распределённости терминов. Для начала объясним, что это за характеристика. Термин называют распределённым, если в высказывании речь идёт обо всех объектах, входящих в его объём. Соответственно, термин не распределён, если в высказывании речь идёт не обо всех объектах, составляющих его объём. Грубо говоря, термин распределён, если мы говорим обо всех предметах, и не распределён, если мы говорим только о некоторых предметах, о части объёма термина.

Давайте возьмём типы высказываний и посмотрим, какие термины в них распределены, а какие нет. Распределённый термин отмечается знаком «+», нераспределённый – знаком «–».

Все S⁺ есть P^–.

Ни один S⁺ не есть P⁺.

Некоторые S^– есть P^–.

Некоторые S^– не есть P⁺.

а⁺ есть P^–.

a⁺ не есть P⁺.

Как видно, субъект всегда распределён в общих и единичных высказываниях, но не распределён в частных. Предикат всегда распределён в отрицательных высказываниях, но не распределён в утвердительных. Если теперь перенести это на наши правила для терминов, то получается, что средний термин хотя бы в одной из посылок должен быть взят во всём своём объёме.

Пингвины – это птицы.
Некоторые птицы не умеют летать.
Пингвины не умеют летать.

Хотя и высказывания над чертой и высказывание под чертой истинны, умозаключение как таковое здесь отсутствует. Здесь нет логического перехода от посылок к заключению. И это можно легко выявить, так как средний термин «птицы» ни разу не берётся во всём своём объёме.

Что касается третьего правила терминов, если в посылках речь идёт только о части объектов из объёма терминов, то в заключении мы не можем ничего утверждать обо всех объектах объёма терминов. Мы не может перейти от части к целому. Кстати, обратный переход возможен: если мы говорим обо всех элементах объёма терминов, то мы можем сделать заключение о части из них.

Энтимемы

Во время реальных дискуссий и споров мы довольно часто опускаем те или иные части рассуждения. Это приводит к возникновению энтимем. Энтимема – это сокращённая форма умозаключения, в которой пропущены посылки или заключение. Важно не путать энтимемы с однопосылочными умозаключениями. Энтимема – это именно многопосылочное умозаключение, просто его части в силу тех или иных причин опущены. Иногда такие пропуски оправданы, так как оба собеседника хорошо разбираются в проблеме, и им нет нужды проговаривать все шаги. Между тем, недобросовестные собеседники могут специально пользоваться энтимемами, чтобы затемнить и запутать своё рассуждение и скрыть свои истинные аргументы или выводы. Поэтому необходимо уметь отличать корректные энтимемы от некорректных. Энтимема называется корректной, если она может быть восстановлена в виде правильного модуса категорического силлогизма, и если все пропущенные посылки оказываются истинными.

Поговорим о том, как восстановить энтимему до полного силлогизма. В первую очередь нужно понять, что именно пропущено. Для этого нужно обратить внимание на слова-маркеры, обозначающие причинно-следственные связи: «таким образом», «следовательно», «так как», «потому что», «в результате» и т.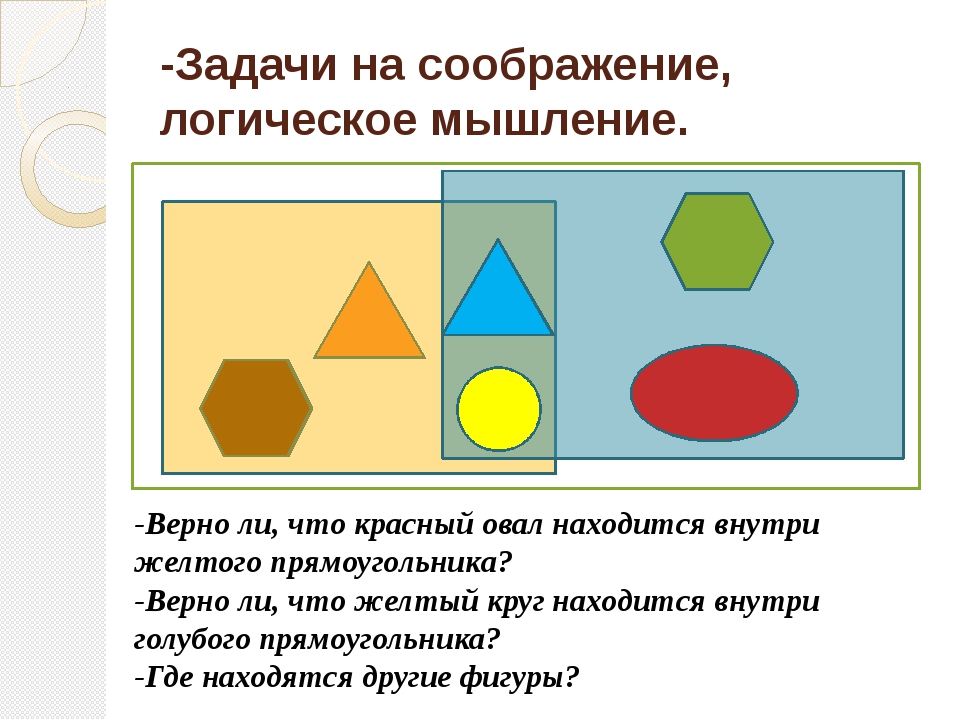 д. К примеру, возьмём рассуждение: «Золото – это драгоценный металл, потому что оно практически не окисляется на воздухе». Здесь заключением является высказывание «Золото – это драгоценный металл». Одна из посылок: «Золото практически не окисляется на воздухе». Ещё одна посылка пропущена. Нужно сказать, что чаще всего пропускают именно одну из посылок. Довольно странно, если в рассуждении отсутствует самое важное – вывод.

Итак, мы установили, что именно пропущено. В нашем примере – это посылка. Большая это посылка или меньшая? Как вы помните, меньшая посылка содержит субъект заключения («золото»), а большая – предикат заключения («драгоценный металл»). Посылка, содержащая субъект заключения нам уже известна: «Золото практически не окисляется на воздухе». Значит, нам известна меньшая посылка, и не известна большая. Кроме того, благодаря известной посылке, мы можем установить и средний термин: «металлы, которые практически не окисляются на воздухе», – тот термин, который не содержится в заключении.

Теперь располагаем известную нам информацию в форме силлогизма:

1.
2. Золото практически не окисляется на воздухе.
3. Золото – это драгоценный металл.

Или в виде схемы:

В большей посылке должны находиться предикат заключения и средний термин: «драгоценные металлы» (P) и «металлы, которые окисляются на воздухе» (M). Здесь возможны два варианта:

Или:

Значит, возможен силлогизм либо второй фигуры, либо первой фигуры. Теперь смотрим на нашу табличку с правильными модусами силлогизмов. Во второй фигуре вообще нет правильных модусов, где в заключении стояло бы высказывание типа а. В первой фигуре есть только один такой модус – Barbara. Достраиваем наш силлогизм:

Или:

1. Все металлы, которые практически не окисляются на воздухе, являются драгоценными.
2. Золото практически не окисляется на воздухе.
3. Золото – драгоценный металл.

Теперь проверяем, истинна ли наша восстановленная посылка. В нашем случае она истинна, поэтому энтимема была правильной.

Сориты

Термином «сориты» пользовался Льюис Кэррол для обозначения сложных силлогизмов, которые имеют более чем две посылки. По большому счёту, сорит представляет собой гибрид силлогизма и энтимемы. Он устроен следующим образом: дано множество посылок, из каждой пары посылок делаются промежуточные выводы, которые обычно опускаются, к промежуточным выводам присоединяются новые посылки, из них делаются новые промежуточные выводы, к которым опять присоединяются новые посылки и так далее, пока мы не переберём все имеющиеся посылки и не дойдём до окончательного заключения. В принципе подобным образом люди и рассуждают в повседневной жизни. Поэтому очень важно уметь решать сориты и оценивать, правильны они или нет.

Мы приведём пример сорита из книги Льюиса Кэррола «История с узелками»:

1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Человек с длинными волосами не может не быть поэтом.
3. Амос Джадд никогда не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. В этой округе нет других поэтов, кроме полисменов.
6. С нашей кухаркой не ужинает никто, кроме её кузенов.
7. Все люди с короткими волосами сидели в тюрьме.

8. Амос Джадд любит холодную баранину.

Над чертой находятся посылки, под чертой – заключение.

Как же нужно решать и проверять сориты? Дадим пошаговую инструкцию. Во-первых, необходимо привести все посылки в более или менее стандартную форму:

1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Все люди с длинными волосами являются поэтами.
3. Амос Джадд не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. Все поэты из нашего округа являются полисменами.
6. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
7. Все люди с короткими волосами сидели в тюрьме.

Теперь нужно взять две исходные посылки. По большому счёту, неважно, с каких именно посылок вы начнёте. Главное, чтобы ваши исходные посылки вместе содержали всего три термина. Это означает, что мы не можем взять посылки «Амос Джадд не сидел в тюрьме» и «Все кузены нашей кухарки любят холодную баранину». В них входят четыре разных термина, а потому мы не можем сделать из них никакого заключения. Я в качестве исходных возьму посылки 7 и 3 и сделаю из них вывод по правилам для простых категорических силлогизмов.

1. Все люди с короткими волосами сидели в тюрьме.
2. Амос Джадд не сидел в тюрьме.
3. Амос Джадд не является человеком с короткими волосами.

Этот силлогизм соответствует модусу Camestres (aee) второй фигуры. Теперь для удобства я переформулирую наш промежуточный вывод следующим образом: «Амос Джадд является человеком с длинными волосами». Этот промежуточный вывод я соединяю с посылкой номер 2:

1. Все люди с длинными волосами являются поэтами.
2. Амос Джадд является человеком с длинными волосами.
3. Амос Джадд является поэтом.

Этот силлогизм соответствует модусу Barbara (aaa) первой фигуры. Теперь я присоединяю этот промежуточный вывод к посылке номер 5:

1. Все поэты из нашего округа являются полисменами.
2. Амос Джадд является поэтом.
3. Амос Джадд является полисменом.

Этот силлогизм опять же соответствует модусу Barbara (aaa) первой фигуры. Присоединяем промежуточный вывод к посылке номер 1:

1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Амос Джадд является полисменом.
3. Амос Джадд ужинает у нашей кухарки.

Это силлогизм, как вы уже, наверное, заметили, тоже представляет собой модус Barbara (aaa) первой фигуры. Присоединяем этот вывод к посылке номер 6:

1. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
2. Амос Джадд ужинает у нашей кухарки.
3. Амос Джадд приходится кузеном нашей кухарке.

Опять Barbara, которая является одним из самых распространённых модусов. Присоединяем к нашему последнему промежуточному выводу последнюю посылку номер 4:

1. Все кузены нашей кухарки любят холодную баранину.
2. Амос Джадд приходится кузеном нашей кухарке.
3. Амос Джадд любит холодную баранину.

Итак, с помощью всё того же модуса Barbara мы получили наше заключение: «Амос Джадд любит холодную баранину». Таким образом, сориты решаются и проверяются с помощью пошагового разделения на простые категорические силлогизмы. В нашем примере сорит оказался правильным, но возможны и обратные ситуации. Существует два условия корректности соритов. Во-первых, каждый сорит должен разбиваться на последовательность правильных модусов силлогизмов. Во-вторых, заключение, которое вы получаете, когда все посылки исчерпаны, должно совпасть с заключением сорита. Это условие действует в тех случаях, когда вы имеете дело с чужим рассуждением, в котором уже присутствует какое-то заключение.

Итак, мы рассмотрели различные многопосылочные умозаключения на примере простых категорических силлогизмов, энтимем и соритов. По большому счёту, если вы знаете, как иметь с ними дело, то вы вооружены для любых дискуссий с любыми противниками. Единственное, что может на данный момент вызывать некоторое недовольство, это необходимость тратить много времени на проверку правильности умозаключений. Не стоит расстраиваться по этому поводу: лучше выглядеть тугодумом, который рассуждает правильно, чем блестящим демагогом, который не замечает своих и чужих ошибок. Тем более, с накоплением опыта внимательного отношения к умозаключениям у вас появится чутьё, автоматический навык, позволяющий быстро отделять корректные рассуждения от некорректных. Поэтому упражнений к этому уроку будет много, чтобы у вас была возможность набить руку.

Задачи Эйнштейна

Эта игра является нашей версией всемирно известной «загадки Эйнштейна», в которой 5 иностранцев живут на 5 улицах, едят 5 видов еды и т.д. Подробнее про эту задачу написано здесь. В подобных заданиях вам нужно сделать правильное умозаключение на основе имеющихся посылок, которых, на первый взгляд, для этого недостаточно.

Упражнения

Упражнения 1, 2 и 3 взяты из книги Льюиса Кэррола «История с узелками», М.: Мир, 1973.

Упражнение 1

Сделайте заключения из следующих посылок по правилам для простого категорического силлогизма. Помните, что простой категорический силлогизм должен содержать только три термина. Не забывайте приводить высказывания к стандартному виду.

Зонтик – очень нужная вещь в путешествии.
Отправляясь в путешествие, всё лишнее следует оставлять дома.
?

Музыка, которую можно услышать, вызывает колебания воздуха.
Музыка, которую нельзя услышать, не стоит того, чтобы за неё платили деньги.
?

Ни один француз не любит пудинга.
Все англичане любят пудинг.
?

Ни один старый скряга не жизнерадостен.
Некоторые старые скряги тощи.
?

Все непрожорливые кролики чёрные.
Ни один старый кролик не склонен к воздержанию в пище.
?

Ничто разумное никогда не ставило меня в тупик.
Логика ставит меня в тупик.
?

Ни в одной из исследованных до сих пор стран не обитают драконы.
Неисследованные страны пленяют воображение.
?

Некоторые сны ужасны.
Ни один барашек не внушает ужаса.
?

Ни одному лысому созданию не нужна расчёска.
Ни у одной ящерицы нет волос.
?

Все яйца можно разбить.
Некоторые яйца сварены вкрутую.
?

Упражнение 2

Проверьте, правильны ли следующие рассуждения. Попробуйте разные способы проверки. Не забывайте ставить большую посылку на первую строку.

Словари полезны.
Полезные книги высоко ценятся.
Словари высоко ценятся.

Золото тяжёлое.
Ничто, кроме золота, не сможет заставить его замолчать.
Ничто лёгкое не сможет заставить его замолчать.

Некоторые галстуки безвкусны.
Всё, сделанное со вкусом, приводит меня в восторг.
Я не в восторге от некоторых галстуков.

Ни одно ископаемое животное не может быть несчастно в любви.
Устрица может быть несчастна в любви.
Устрицы – не ископаемые животные.

Ни одна горячая сдоба не полезна.
Все булочки с изюмом неполезны.
Булочки с изюмом – не сдоба.

Некоторые подушки мягкие.
Ни одна кочерга не мягкая.
Некоторые кочерги – не подушки.

Скучные люди невыносимы.
Ни одного скучного человека не упрашивают остаться, когда он собирается уходить из гостей.
Ни одного невыносимого человека не упрашивают остаться, когда он собирается уходить из гостей.

Ни одна лягушка не имеет поэтической внешности.
Некоторые утки выглядят прозаично.
Некоторые утки – не лягушки.

Все разумные люди ходят ногами.
Все неразумные люди ходят на голове.
Ни один человек не ходит на голове и ногах.

Упражнение 3

Найдите заключения следующих соритов.

Малые дети неразумны.
Тот, кто может укрощать крокодилов, заслуживает уважения.
Неразумные люди не заслуживают уважения.

Ни одна утка не танцует вальс.
Ни один офицер не откажется потанцевать вальс.
У меня нет другой птицы, кроме уток.

Всякий, кто находится в здравом уме, может заниматься логикой.
Ни один лунатик не может быть присяжным заседателем.
Ни один из ваших сыновей не может заниматься логикой.

В этой коробке нет моих карандашей.
Ни один из моих леденцов – не сигара.
Вся моя собственность, не находящаяся в этой коробке, состоит из сигар.

Ни один терьер не блуждает среди знаков Зодиака.
То, что не блуждает среди знаков Зодиака, не может быть кометой.
Только у терьера хвост колечком.

Никто не станет выписывать газету «Таймс», если он не получил хорошего образования.
Ни один дикобраз не умеет читать.
Те, кто не умеет читать, не получили хорошего образования.

Никто их тех, кто действительно ценит Бетховена, не станет шуметь во время исполнения «Лунной сонаты».
Морские свинки безнадёжно невежественны в музыке.
Те, кто безнадёжно невежественен в музыке, не станут соблюдать тишину во время исполнения «Лунной сонаты».

Вещи, продаваемые на улице, не имеют особой ценности.
Только дрянь можно купить за грош.
Яйца большой гагарки представляют большую ценность.
Лишь то, что продаётся на улице, и есть настоящая дрянь.

Те, кто нарушает свои обещания, не заслуживают доверия.
Любители выпить очень общительны.
Человек, выполняющий свои обещания, честен.
Ни один трезвенник не ростовщик.
Тому, кто очень общителен, всегда можно верить.

Любая мысль, которую нельзя выразить в виде силлогизма, поистине смешна.
Моя мечта о сдобных булочках не стоит того, чтобы её записывать на бумаге.
Ни одну мою несбыточную мечту нельзя выразить в виде силлогизма.
Мне не приходило в голову ни одной действительно смешной мысли, о которой я бы не сообщим своему другу.
Я только и мечтаю, что о сдобных булочках.
Я никогда не высказывал своему другу ни одной мысли, если она не стоила того, чтобы её записать на бумаге.

Упражнение 4

Проверьте правильность следующих энтимем.

Барсик – не законопослушный кот, потому что он украл у меня сосиску.
Ртуть жидкая, следовательно, она не может быть металлом.
Ни один послушный ребёнок не устраивает истерик по пустякам. Поэтому Толя – непослушный ребёнок.
Некоторые женщины глупы, значит, некоторые мужчины могут этим воспользоваться.
Все девушки хотят выйти замуж, так как каждая из них мечтает о пышном белом платье.
Ни один студент не хочет получить двойку на экзамене, вот почему все студенты – ботаники.
Некто украл у меня кошелёк, поэтому у меня совсем не осталось денег.
Павлины – самовлюблённые птицы, потому что у них большой красивый хвост.

Проверьте свои знания

Ксения Галанина

Урок 4. Суждения и высказывания. Введение в силлогистику

В прошлых уроках рассказывалось о том, как правильно работать с понятиями и определениями. Хотя операции над ними очень важны и встречаются повсеместно, сами по себе они ещё не составляют рассуждений. В этом уроке мы как раз приблизимся к теме того, как правильно рассуждать. Мы будем рассматривать рассуждения на примере силлогистики. Силлогистика – это самая древняя логическая система. Она была изобретена древнегреческим философом Аристотелем в IVвеке до н.э. До сих пор она остаётся одной из самых понятных, приближенных к естественному языку и лёгких для изучения логических систем. Одно из главных её достоинств – возможность применения в повседневных ситуациях без особых усилий.

Содержание:

Суждения и высказывания
Состав и виды категорических атрибутивных высказываний
Условия истинности для категорических атрибутивных высказываний в традиционной силлогистике
Игра «Пересечение множеств»
Упражнения
Проверочные вопросы на усвоение материала

Суждения и высказывания

Что такое рассуждение? Можно было бы сказать: вывод, умозаключение, размышление, доказательство и т.д. Всё это верно, но, пожалуй, самым очевидным ответом было бы: рассуждение – это последовательность суждений, которые в идеале должны быть связаны между собой согласно правилам логики. Поэтому обучение правильному рассуждению нужно начинать с того, что такое суждения и как ими корректно пользоваться.

Суждение – это мысль об утверждении или отрицании наличия некоторой ситуации в мире.

В естественном языке суждения передаются с помощью повествовательных предложений, или высказываний. Примеры суждений, выраженных в высказываниях: «Пришла осень», «Катя не знает английского языка», «Я люблю читать», «Трава зелёная, а небо голубое». Одно и то же суждение может быть выражено с помощь разных высказываний, в частности: «Небо голубое» и «The sky is blue» – разные высказывания, но суждение они выражают одно и то же, так как они передают одну и ту же мысль. Точно также высказывания «Никто не покидал дома» и «Все оставались дома» разные, но они передают одно суждение.

Поскольку высказывания посредством суждений фиксируют какое-то положение дел в мире, в отличие от понятий и определений, мы можем оценивать их с точки зрения их истинности и ложности. Так высказывание «Бил Гейтс основал компанию “Microsoft”» – истинное, а высказывание «Апельсины фиолетовые» – ложное.

Если вспомнить треугольник Фреге, то высказывание будет находиться на вершине, обозначающей знак, суждение будет составлять его смысл, а истина и ложь – значение.

Существует множество типов суждений и, соответственно, высказываний. Разные логические системы концентрируются на их разных аспектах. Силлогистика работает с так называемыми категорическими атрибутивными высказываниями. Категорические высказывания противопоставляются гипотетическим. Гипотетические высказывания говорят о возможности наличия или отсутствия какой-то ситуации в мире: «Возможно, пойдёт дождь». Категорические высказывания безапелляционно утверждают о том, что какая-то ситуация имеется или не имеется: «Пошёл дождь». Термин «атрибутивный» означает, что эти высказывания говорят о наличии либо отсутствии у предмета или класса предметов некоторого свойства. Примеры категорических атрибутивных высказываний: «Моя машина синего цвета», «Парк около нашего дома большой», «Никто не любит рыбий жир», «Некоторые люди считают, что они самые умные». Хотя на первый взгляд может показаться, что из-за концентрации именно на категорических атрибутивных высказываниях, применение силлогистики ограничено, это не так. Огромный пласт рассуждений не выходит за рамки подобных высказываний, а потому знания силлогистики оказывается достаточно для того, чтобы научиться размышлять логично и не давать ввести себя в заблуждение.

Состав и виды категорических атрибутивных высказываний

Категорические атрибутивные высказывания состоят из терминов, предицирующих связок и кванторов.

Термины делятся на субъект и предикат.

Субъект – это термин, обозначающий предмет или группу предметов, о которых нечто утверждается или отрицается. Обычно субъект изображается с помощью буквы S.
Предикат – это термин, обозначающий собственно то, что утверждается или отрицается о субъекте, некоторое свойство, признак, наличие или отсутствие которого приписывается субъекту. Предикат изображается с помощью буквы P.

Предицирующие связки, как, возможно, вы помните из первого урока, это связки «есть» и «не есть». В естественном языке они могут выражаться с помощью разных слов и конструкций: «есть», «являться», «суть», «это», «выступать», знака тире, глаголов, либо вообще опускаться.

Кванторы – это слова, указывающие на количественные характеристики субъекта. Существует два вида кванторов: квантор общности («все», «каждый», «любой», «ни один», «никто») и квантор существования («некоторые», «не все», «какой-либо», «многие»). Также как и предицирующие связки, кванторы в естественной речи могут опускаться. Мы можем сказать: «Люди равны перед законом», подразумевая, что «Все люди равны перед законом»; или «Дети любят сладкое» – подразумевая, что «Многие дети любят сладкое». Зачастую лучше всего уточнить у вашего собеседника, какой именно квантор он имеет в виду, так как это будет сказываться на условиях истинности его высказываний.

Давайте разберём следующее высказывание: «Кошки мурлычут, когда им приятно». «Кошки» – это субъект, «существа, мурлычущие, когда им приятно» – это предикат. Также здесь присутствует невидимая связка «есть», которая соединяет субъект с предикатом, и невидимый квантор общности «все». Так, если записать это высказывание в соответствии с его логической формой, то получим: «Все кошки есть существа, которые мурлычут, когда им приятно». Благодаря этому примеру становится ясно, что прежде чем определять, истинно высказывание или ложно, нужно выявить его логическую форму и преобразовать исходное высказывание так, чтобы все четыре элемента (квантор, субъект, связка, предикат) были на своих местах.

В зависимости от свойств логических и нелогических терминов, входящих в состав категорических атрибутивных высказываний, их можно разделить на несколько видов.

В зависимости от характера субъекта категорические атрибутивные высказывания делятся на единичные и множественные. Если в качестве субъекта выступает имя, то речь идёт о единичном высказывании («Сократ был философом»). Единичные высказывание не имеют квантора перед субъектом. Если же субъект – это термин, обозначающий множество предметов, то высказывание называют множественным. Множественные высказывания в свою очередь делятся на частные и общие в зависимости от того квантора, который стоит перед ним. Если используется квантор существования, то высказывание будет частным («Некоторые девушки красивы»), если квантор общности – то общим («Все люди стремятся к счастью»).
В зависимости от предицирующей связки высказывания делятся на утвердительные и отрицательные. Если утверждается наличие какого-то свойства у субъекта, то высказывание утвердительное («Петя – настоящий друг»), если отрицается – то отрицательное («Ни один студент не пришёл на первую пару!»).

Если мы скомбинируем эти виды между собой, то получается, что всего существует шесть видов категорических атрибутивных высказываний:

Единичноутвердительные: s есть P. Александр Пушкин – это русский писатель.
Единичноотрицательные: s не есть P. Сервантес не был художником.
Общеутвердительные: Все S есть P. Все квартиры в этом доме имеют высокие потолки.
Общеотрицательные: Ни один S не есть P. Ни один студент из нашей группы не сдал экзамен на пятёрку.
Частноутвердительные: Некоторые S есть P. Некоторые машины из нашего автопарка нуждаются в срочном ремонте.
Частноотрицательные: Некоторые S не есть P. Некоторые тексты песен не имеют смысла.

Условия истинности для категорических атрибутивных высказываний в традиционной силлогистике

Следует начать с того, что традиционная силлогистика накладывает два ограничения на используемые термины, а именно: они должны быть непусты и неуниверсальны, то есть если под термин не подпадает ни один объект из универсума рассмотрения или, наоборот, подпадают все объекты универсума, то они не могут быть предметом рассмотрения. Посмотрим на рисунки:

Первый рисунок изображает ситуацию, когда термин А пуст, поэтому весь квадратик (универсум рассмотрения) остался белым. Второй рисунок показывает случай, когда объём термина А совпадает с объёмом универсума рассмотрения, поэтому весь квадрат заштрихован. Последний рисунок репрезентирует термин А, который является непустым и в то же время неуниверсальным. Заштрихованая область соотвествует объёму А. Традиционная силлогистика работает только с терминами, которые соотвествуют третьему рисунку. Такое условие ставится для того, чтобы исключить из рассмотрения высказывания, которые невозможно оценить как истинные либо ложные. Возьмём высказывание: «Все дети Ивана лысые». Вроде бы с высказыванием всё впорядке, однако представьте, что у Ивана нет детей. Мы не можем в данном случае просто сказать, что высказывание ложное. Если назвать его ложным, то тем самым мы подразумеваем, что не все дети Ивана лысые, а это не так. В то же время мы не можем сказать, что оно истинное. Выход из этого затруднительного положения состоит как раз в том, чтобы указать на пустоту термина «дети Ивана». Поскольку у Ивана нет детей, этот термин пуст, и мы не можем построить с ним корректное высказывание.

Непустота и неуниверсальность термина будут определяться не только контекстом, но и выбранным универсумом рассмотрения. Если наш квадратик представляет собой универсум живых существ или материально существующих предметов, то, конечно, такие термины как «русалка», «хоббит», «дракон» и т.п. окажутся пустыми, и мы не сможем их рассматривать. Однако, если универсум рассмотрения – это мифологические или сказочные существа, то все эти термины перестают быть пустыми. То же самое верно и для универсальности. Термин «люди» может рассматриваться как универсальный, что исключает его из области традиционной силлогистики. Однако если мы хотим сказать «Сократ – человек», то в качестве универсума рассмотрения вполне можно взять живых существ. На универсуме живых существ, термин «люди» уже не будет универсальным.

Кроме того, нужно помнить, что субъект и предикат должны задаваться на одном и том же универсуме рассмотрения.

Теперь посмотрим, при каких условиях разные типы категориальных атрибутивных высказываний будут истинными. Для этого советуем ещё раз заглянуть в урок, посвящённый отношениям между понятиями. По большому счёту, субъект и предикат – это термины, представляющие некоторые понятия. Соответственно, если соединить эти понятия в одном предложении с помощью предицирующих связок и кванторов, то, чтобы узнать будут эти предложения истинными или ложными, достаточно посмотреть на диаграммы, иллюстрирующие отношения между этими двумя понятиями. Итак, преступим.

Единичноутвердительные высказывания формы «s есть P» истинны, только если термины s и P находятся в следующем отношении:

Другими словами, единичноутвердительные высказывания истинны, если точка, представляющая собой имя s, находится внутри кружочка, изображающего объём термина P. Например, возьмём высказывание «Лев Толстой проповедовал вегетарианство». «Лев Толстой» – это субъект, имя s. «Человек, проповедующий вегетарианство» – это предикат, термин P. Это высказывание истинно, так как точка s будет входить в объём термина P. Если же взять высказывание «Николай Гоголь – это великий русский композитор», то точка s, представляющая имя («Николай Гоголь»), не будет входить в объём термина P («великие русские композиторы»). Поэтому это высказывание ложно.

Единичноотрицательные высказывания, имеющие форму «s не есть P» истинны, если термины s и P находятся в следующем отношении:

Как видно из рисунка, здесь имеет место ситуация, прямо противоположная условиям истинности единичноутвердительных высказываний. Если точка, представляющая имя s, находится вне объёма термина P, то высказывание истинно. В обратном случае, оно ложно. Пример истинного единичноотрицательного высказывания: «Александр Пушкин никогда не был во Франции». Ложным единичноотрицательным высказыванием будет: «Иван Бунин не получил Нобелевскую премию по литературе».

Общеутвердительные высказывания формы «Все S есть P» истинны, если термины S и P находятся в одном из следующих отношений:

Первый рисунок изображает отношение равнообъёмности, второй – обратного подчинения. Если объёмы двух терминов совпадают (S и P делят один кружочек) или объём термина S полностью входит в объём термина P (кружочек S полностью включается в P), то общеутвердительное высказывание истинно. Если термины S и P находятся в каком-либо другом отношении, то общеутвердительные высказывания не могут быть истинными. В качестве иллюстрации истинных высказываний можно привести: «Все хвойные растения имеют шишки», «Все киты – это млекопитающие». Пример ложных высказываний: «Все политики – обманщики», «Все девушки мечтают выйти замуж за миллионера». В этих примерах термины, обозначающие субъект и предикат, не находятся ни в одном из указанных выше отношений.

Общеотрицательные высказывания, имеющие форму «Ни один S не есть P» истинны, только если термины S и P находятся в следующих отношениях:

На первом рисунке представлено отношение противоречия, а на втором – соподчинения. Как видно, у S и P нет общих элементов, их объёмы не пересекаются. К примеру, истинными будут высказывания: «Ни один павлин не относится к числу певчих птиц», «Ни один человек младше восемнадцати лет не является совершеннолетним в России». Пример ложного высказывания: «Ни один гуманитарий не разбирается в математике». Высказывание ложно, так как термины «гуманитарий» и «люди, разбирающиеся в математике» не находятся ни в отношении противоречия, ни в отношении соподчинения.

Частноутвердительные высказывания формы «Некоторые S есть P» истинны, если термины S и P находятся в следующих отношениях:

Рисунки последовательно представляют отношения: пересечения, дополнительности, подчинения, равнообъёмности и обратного подчинения. С первыми тремя картинками всё должно быть довольно ясно: видно, что объёмы терминов S и P пересекаются, поэтому в области пересечения находятся элементы, которые одновременно обладают и признаком S и признаком P. Примеры истинных высказываний таких типов: «Некоторые актёры хорошо поют», «Некоторые автомобили с ценой ниже миллиона стоят больше шестисот тысяч», «Некоторые грибы съедобны».

Что касается отношений равнообъёмности и обратного подчинения, то может возникнуть вопрос, почему они тоже представляют собой условия истинности для частноутвердительных высказываний, если на картинках, обозначающих их, чётко видно, что не только некоторые S есть P, но все S есть P. Правда, естественный язык толкает нас к идее, что если некоторые S есть P, то ещё существуют и другие S, которые не есть P: некоторые грибы съедобны, а некоторые несъедобны. Для логиков такое заключение неверно. Из высказывания «Некоторые S есть P» нельзя вывести заключение, что некоторые S не есть P. Зато из высказывания «Все S есть P» можно заключить, что и некоторые S есть P, потому что если что-то верно относительно всех элементов объёма термина, то оно будет верно и относительно некоторых отдельных элементов. Поэтому в силлогистике слово «некоторые» употребляется в значении «по крайней мере некоторые», но не в значении «только некоторые». Таким образом, из высказывания «Все папоротники размножаются спорами» можно смело вывести и высказывание «Некоторые папоротники размножаются спорами», а из высказывания «Все ученики пятого класса являются пионерами» – высказывание «Некоторые ученики пятого класса являются пионерами».

Частноутвердительные высказывания будут ложными, только если термины S и P находятся в отношении противоречия или соподчинения: «Некоторые тракторы – это самолёты», «Некоторые ложные высказывания истинны».

Частноотрицательные высказывания типа «Некоторые S не есть P» истинны, если термины S и P находятся в следующих отношениях:

Это отношения: пересечения, дополнительности, включения, противоречия и соподчинения. Очевидно, что первые три отношения совпадают с тем, что было верно и для частноутвердительных высказываний. Все они как раз представляют случаи, когда некоторые S есть P, и в то же время некоторые S не есть P. Примеры подобных истинных высказываний: «Некоторые здоровые люди не употребляют алкоголь», «Некоторые наши работники из категории младше сорока ещё не достигли возраста и двадцати пяти», «Некоторые деревья не являются вечнозелёными».

По тем же причинам, по которым отношения равнообъёмности и обратного подчинения представляли собой условия истинности для частноутвердительных высказываний, отношения противоречия и соподчинения будут верны для частноотрицательных высказываний. Из высказывания, имеющего форму «Некоторые S не есть P» нельзя логично вывести высказывание «Некоторые S есть P». Однако из высказывания «Все S не есть P» можно перейти к высказыванию «Некоторые S не есть P», так как на основании информации, которой мы обладаем обо всех элементах объёмов терминов S и P, можно сделать вывод и об их отдельных представителях. Поэтому верными будут высказывания: «Некоторые журналы не являются книгами», «Некоторые глупцы не являются умными» и т.п.

Частноотрицательные высказывания будут ложными, только если термины S и P находятся в отношениях равнообъёмности и обратного подчинения. Примеры ложных высказываний: «Некоторые рыбы не умеют дышать под водой», «Некоторые яблоки не являются фруктами».

Итак, мы выяснили, при каких условиях высказывания той или иной формы будут истинными и ложными. При этом стало понятно, что не всегда истинность и ложность высказываний с логической точки зрения совпадает с нашими интуитивными представлениями. Иногда одинаковые на первый взгляд высказывания оцениваются совершенно по-разному, так как за ними скрываются разные логические формы и, следовательно, разные отношения между входящими в них терминами. Эти условия истинности важно запомнить. Они пригодятся, когда в следующем уроке мы научимся складывать высказывания в цепочки рассуждений и будем пытаться найти такие формы умозаключений, которые будут всегда правильными.

Игра «Пересечение множеств»

В этом упражнении вам нужно внимательно прочитать текст задания и правильно расположить множества, соответствующие понятиям.

Упражнения

Прочитайте следующие категориальные атрибутивные высказывания. Определите, к какому типу они относятся. С помощью диаграмм покажите, истинны они или ложны.

Всё действительное разумно, всё разумное действительно.
Соль – это яд.
Яд – это соль.
Все музыканты имеют хороший слух.
Некоторые музыканты имеют хороший слух.
Все люди, имеющие хороший слух, – музыканты.
Некоторые люди, имеющие хороший слух, – музыканты.
Некоторые вампиры опоздали на работу.
Волколаки – это разновидность оборотней.
Все круглые квадраты не имеют углов.
Никто не любит, когда у него болят зубы.
Ни один попугайчик не пьёт виски.
Некоторым не нравится их работа.
Иван Иванович поссорился с Иваном Никифоровичем.
Фильмы Тарковского считаются классикой русского кино.
Достоевский никогда не играл в карты.
Некоторые куздры совсем не глокие.
Каждый сотрудник мечтает о повышении.
Некоторые псы умеют читать.
Все счастливые семьи похожи друг на друга, каждая несчастливая семья несчастлива по-своему.
Некоторые акулы – это рыбы.
Некоторые люди не летали на Марс.

Проверьте свои знания

Ксения Галанина

6 способов развить логическое мышление, если ты гуманитарий | GeekBrains

«Перепрошить» можно любой мозг.

https://d2xzmw6cctk25h.cloudfront.net/post/1623/og_cover_image/ec98f22ccd4cc9ae9a0bdd6ff0345abc

«Перепрошить» можно любой мозг. Всё благодаря нейропластичности — свойству меняться под воздействием опыта. И да, заголовок — кликбейт. Нет прирожденных «гуманитариев» и «технарей», есть только лень. Мы уже рассказывали, как развивать логическое мышление. В этой статье — ещё несколько советов.

Спорьте!

Всегда ли вы можете доказать мнение, подобрав нужные аргументы? Бывало ли, что не получалось объяснить — чем фильм, который вы предлагаете посмотреть, лучше варианта друзей? Умение доказывать свою позицию не только полезно и выгодно (если речь о том, чтобы торговаться или аргументировать повышение зарпалты), но и развивает логику. Подбирая аргументы, анализируешь причины и следствия.

Постоянно нарываться на спор в бытовых ситуациях не нужно. Пойдите на лекцию, мастер-класс, в клуб-любителей-чего-угодно и участвуйте в горячих дискуссиях. Попробуйте мысленно или вслух, в дружеской компании, доказывать случайные тезисы. Например, аргументируйте, что «Дэдпул-2» — интеллектуальное кино. Для тренировки. Участвуйте в рэп-баттлах и спорьте с людьми в интернете, в конце концов.

Спрашивайте себя «что?», «как?» и «почему?»

Упражнение, которое можно делать где и когда угодно:

Выбираете случайный объект и задаете эти три вопроса относительно него;
Четко и логично отвечаете на них. Если не получается — гуглите. Эта привычка — отдельный бонус, который увеличивает шансы стать крутым айтишником;
Переходите к следующему объекту.

Слишком просто? Попробуйте! Удивитесь, сколько интересного не замечали.

Практикуйте SWOT-анализ

SWOT — это оценка сильных (Strengths) и слабых (Weaknesses) сторон, а также возможностей (Opportunities) и угроз (Threats) чего бы то ни было: идеи, предложения, объекта.

Как это делается, проще объяснить на примере. Допустим, вы подумываете поужинать в фаст-фуде. Сильные стороны: быстро, дешево, вкусно. Слабые: вредно, калорийно. Возможности: не надо готовить, освободится время на изучение программирования. Угрозы: можно отравиться или просто объесться, и ничего делать уже не захочется. Можно так же проанализировать вариант «писать код сейчас» или «взять ещё один фриланс». И сделать рациональный выбор.

Играйте в видеоигры

Чтобы развивать логику, не обязательно упражняться в скучных специализированных приложениях — решать головоломки и складывать пазлы. Прокачивать мозг можно, играя практически в любую стратегию, — например, «Starcraft» или «Civilization». Даже «Call of Duty» развивает способность к решению задач. Главное, чтобы игры не были единственным занятием — для тренировки мозга достаточно играть 3 раза в неделю по 20 минут.

Изучайте логику

Не спешите звать Капитана Очевидность. Многие забывают, что логика — наука, и её можно изучать. Олег Иванов, психолог, руководитель Центра урегулирования социальных конфликтов, советует начать с трудов Рене Декарта: «Изучение научных трудов мыслителей и философов способствует развитию логического мышления. Полезно и самому писать научные статьи. Использование индукции и дедукции в такой работе позволяет выработать алгоритм. Обобщение, анализ, вывод — всё это способствует развитию логического мышления».

От себя (ура, диплом философа пригодился!) рекомендую почитать Аристотеля. А тем, кто хочет поставить сложность на максимум, советую «Науку логики» Гегеля. Ещё можно разобраться, что такое круги Эйлера:

Шутка, основанная на кругах Эйлера.

Измеряйте неизмеримое — решайте задачи Ферми

Великий математик Энрико Ферми (тот самый, что знаменит парадоксом) считал, что за 60 секунд можно оценить абсолютно всё. Нужно знать лишь несколько фактов, чтобы примерно посчитать, сколько селфи делается в день на Земле, сколько раз в среднем люди нецензурно выражаются или ответить на другой подобный вопрос.

Объясню на примере. Допустим, вас спросили: «Сколько женщин подрабатывает, делая маникюр в Питере?». Чтобы дать приблизительный ответ, можно использовать такую логику:

Помню, что в Москве население около 12 миллионов. Питер где-то в 2 раза меньше — пусть будет 6 миллионов;
Половина знакомых девушек делает маникюр у специалиста, около 50% населения — женщины. Значит, в Питере потенциально 1,5 миллиона женщин «делают ноготочки» в салоне;
На маникюр ходят примерно раз в 2 недели — около 26 раз в год. Значит, за год в Питере это будет 1,5 млн * 26 раз = 39 миллионов раз;
На маникюр уходит примерно час — значит, один мастер может за день обслужить 8 клиенток;
Теперь нужно узнать, сколько требуется мастеров, чтобы успеть сделать маникюр 39 миллионов раз за год, при «производительности» 8 клиентов в день на одного специалиста. 39 млн / 365 дней / 8 раз в день = 13 356 мастеров маникюра в Питере.

Конечно, это примерная цифра. Ведь мастера не работают каждый день, и в расчёте не учтены мужчины, которые делают маникюр, дети, а также мужчины-мастера. Наверняка, что-то ещё упущено или перепутано. Но в решении подобных задач важен сам подход. Кстати, такие вопросы любят задавать в крупных компаниях на собеседованиях, чтобы проследить, как человек размышляет, думает ли вообще или сразу сдается и говорит, что задачу решить нереально.

Поэтому предлагаю начать тренироваться. Подумаем логически, сколько людей отказалось от своей мечты в пользу лени?

Как развить логическое мышление? | GeekBrains

Девять способов прокачать свой мозг.

https://d2xzmw6cctk25h.cloudfront.net/post/361/og_cover_image/181e092ebbc5d72d54edfe31e87f97fd

В IT-сфере особенно важно иметь развитые способности к анализу, уметь формализовать любой процесс и выстраивать сложные логические конструкции. Поговорим о том, как разбудить левое полушарие мозга и прокачать аналитическое мышление.

Тренируйтесь с помощью логических игр

Го, шахматы, кубик Рубика, кроссворды, судоку и прочие головоломки — интересный и действенный способ прокачать стратегическое мышление и способность к длительной концентрации.

Рисуйте диаграммы

Левое полушарие мозга отвечает за логику, стремиться понять причинные связи. Правое — за интуицию, восприятие целостной картины, образное мышление. Если логическая «мышца» атрофировалась, то первое время может понадобиться подключать левое полушарие к работе через правое. Тут спасительным кругом послужит образное представление логики вещей с помощью схем, диаграмм, ментальных карт. В дальнейшем, когда необходимые навыки будут развиты, вы сможете выполнять все операции непосредственно в голове.

Задавайте вопросы

Начните с интересом относиться к окружающим вещам, не избегайте вопросов. Старайтесь объективно разобраться — как, почему и зачем работает окружающий мир. Но не стоит использовать этот прием в отношении себя, если вы не хотите увязнуть в самокопании.

Конкретизируйте

Часто задачи кажутся неразрешимыми не из-за того, что вы не способны мыслить логически, а потому что выбирете неправильный подход. Для решения многих «сверхсложных» проблем может сгодиться простой алгоритм. Например, ваша цель — остановить глобальное потепление. Сложно. Но что, если переформулировать цель так — каждый год снижать глобальный выброс углекислого газа на 5%? Уже гораздо проще, осталось только определить основных виновников его высокого поступления в атмосферу и начать действовать. Это работает во всех сферах. То есть, вместо того, чтобы биться над решением абстрактной масштабной задачи, определите, какие мелкие проблемы ее формируют и разберитесь с ними.

Читайте детективы

Погрузившись в детективную историю трудно не начать анализировать ситуацию и не попытаться найти развязку. Конечно, польза будет только от чтения качественной литературы, например, романов Жоржа Сименона или Агаты Кристи.

Упражняйтесь на специальных сайтах

Попробуйте BrainExer, S-mind, Brainscale. Если у вас достаточный опыт программирования, то вы найдете массу полезностей в подборке «26 сайтов с головоломками и обучающими задачами для разработчиков».

Изучайте математику

Выберите любой посильный вам раздел и разберитесь с используемыми в нем концепциями и определениями. Ознакомьтесь с аксиомами и вытекающими из них доказательствами теорем. Перечитывайте их до тех пор, пока не добьетесь полного понимания. Даже если в школьные годы вы не дружили с математикой, то никогда не поздно поднять старые учебники, уже с другой мотивацией и азартом.

Абстрагируйтесь от эмоций

Разделяйте рациональные и эмоциональные решения. Всегда ли вы можете объяснить почему поступаете тем или иным образом? Если вы испытываете затруднения при ответе, то, это эмоциональное решение.

Найдите внутренний баланс

Когда мозг подвержен сильному стрессу, то теряется способность ясно и последовательно мыслить. Перед тем, как начинать умственную работу нужно успокоиться и создать вокруг себя комфортную атмосферу.

А какие способы развить логическое мышление знаете вы?

P. S. Что развивает логическое мышление лучше разработки? Развиться и заработать позволит профессия «Веб-разработчик».

вся логика для дошкольников и младших школьников

Теория

Для формирования словесно-логического мышления мы предлагаем свою теоретическую базу по всем разделам логики, адаптированную для детей младшего школьного возраста. В текстовом формате раскрываем основные понятия, категории и органично дополняем их изображениями, видеоматериалами и примерами заданий с разбором решения.

Таким образом расширяется понятийный аппарат школьника, он учится учиться, выбирать, какие из приобретенных теоретических знаний необходимо использовать при решении конкретной задачи, и применяет их.

Мама и дочка, а также мама и папа заказали разные блюда. Как правильно распределить тарелки?

Авторы и разработчики программы LogicLike учли и такую особенность детского мышления, как нечувствительность к противоречию, из-за чего для детей характерно совершение одной и той же ошибки многократно. Чтобы помочь учащемуся избежать этого и лучше усвоить новый материал, а не просто запомнить правильный ответ, в лаборатории Logic предусмотрены комментарии с логическими рассуждениями к уже выполненным заданиям.

Мотивация и социальный аспект

Психологи утверждают, что у детей с возраста 7-8 лет особенно ярко начинает проявляться стремление к лидерству и накоплению собственных достижений. Поэтому основным мотивом деятельности ребенка становится мотив достижения успеха. Также для младших школьников характерен эгоцентризм, а постоянно обновляемые рейтинги позволяют ему сравнить свои успехи с достижениями других ребят-ровесников, объективно оценить эффективность своих занятий по логике.

Хорошо продуманная система рейтинга и наград за каждое правильно выполненное задание является мощным стимулом для школьника стремиться выполнять упражнения правильно с первой попытки, а значит, серьезно подходить к процессу обучения, размышлять и принимать решения.

В лаборатории Logic дети воспринимают себя частью хорошей компании друзей. Всегда рядом Профессор, который похвалит или заставит задуматься, и Робот Клапан, готовый прийти на помощь дельным советом. В рейтинге ребёнок видит десятки тысяч таких же как он ребят, которые на пути к новым вершинам логики увлеченно решают одну головоломку за другой. На странице достижений родители наблюдают за прогрессом ребёнка.

Система

Более 3500 уникальных задач на развитие логического мышления LogicLike распределены по 17 тематическим разделам. Кроме востребованных в школе текстовых задач на логику, вопросов по темам «Закономерности», «Ложные и истинные высказывания», на сайте десятки других видов заданий: загадки на логическое мышление, головоломки для развития пространственного мышления, адаптированные для детского понимания задания по темам «Алгоритмы» и «Комбинаторика», математические ребусы, упражнения и игры на развитие логического мышления.

В отличие от уроков математики, на ЛогикЛайк ученик может выбрать раздел, который интересует его сегодня. Однако перейти на новый, более сложный уровень нельзя, пока не решены все задачи из предыдущего уровня. Так мы исключаем возможные пробелы знаний, обеспечиваем системность обучения.

Прохождение программы LOGIC обеспечивает формирование у детей гибкого критического мышления и развивает умение мыслить логически. А главное – учебный процесс очень нравится нашим юным любителям логики. И мальчики, и девочки с удовольствием «играют в Лоджик»: выполнение заданий воспринимается как увлекательная компьютерная игра, а не школьный урок.

Занимательные занятия онлайн — современный и эффективный подход к развитию логики у детей и взрослых.

задания и упражнения на развитие логического мышления детей в 1-4 классах

Зачем развивать логику

Развитая логика помогает выделять суть в потоке информации, принимать взвешенные решения и чётко формулировать свои мысли — эти способности пригодятся не только в школе. Во времена высоких технологий умение мыслить логически становится не просто конкурентным преимуществом, а жизненно необходимым навыком. Вот лишь несколько причин, по которым стоит развивать логику:

Чтобы постоянно развиваться. Технологии прогрессируют с огромной скоростью и требует того же от человека. Не оказаться за бортом цивилизации сможет только живой и пластичный ум.
Чтобы правильно формулировать вопросы. Это важнейшее умение и для учёбы, и для жизни вообще. Чтобы получать быстрые и точные ответы, вопросы нужно уметь грамотно задавать.
Чтобы отличать правду ото лжи. Информационное пространство переполнено противоречивыми сведениями. Развитая логика поможет сопоставить факты, сравнить источники и не стать жертвой обмана.
Чтобы находить нестандартные решения. И дело даже не в том, что это ключевой навык для работы в самой высокооплачиваемой сфере — IT. Ни в одной профессии, подразумевающей интеллектуальный труд, не обойтись без изобретательности.

Преподаватель информатики Анастасия Александрова подчёркивает важность развития логики для учёбы.

«Для успешного изучения информатики нужна логика. Если у вас трудности со школьным курсом, потренируйте сначала своё логическое мышление на простейших задачах».

<<Блок перелинковки>>

Способы развития логического мышления

Логическое мышление — это не врождённый талант, его необходимо развивать. Существует много способов, позволяющих делать это с удовольствием. Перечислим лишь некоторые из них:

Логические задачи. Многие задачки на логику придуманы тысячи лет назад, но актуальны до сих пор. Зачастую они сформулированы очень забавно, так что искать остроумные ответы на них весело и увлекательно. Множество таких задач легко найти в интернете.
Интеллектуальные игры. Игра для детей — способ познания мира. Играя с ребёнком в домино, шашки, шахматы, точки, эрудит и даже просто в слова, вы не только весело проводите время, но и развиваете мышление ребёнка.
Головоломки. Специализированные магазины предлагают ассортимент «игр для ума» на любой вкус и возраст — всевозможные лабиринты, пазлы, кубики Рубика и целые научно-исследовательские наборы. Во многих городах работают кружки любителей головоломок, где дети учатся их разгадывать и соревнуются в искусстве решения.
Развивающие сервисы. В Сети существуют специальные платформы, на которых собраны различные задачи на развитие логики у детей. Процесс их решения напоминает игру с разными уровнями сложности.
Компьютерные игры. Вопреки распространённому убеждению, далеко не все они пустая трата времени. В интернете найдётся огромное количество игр на развитие логики — от простейших «Тетриса» и «Лайнс» до «Майнкрафта» с его неисчислимыми возможностями.

Развитие логического мышления в 1 классе

Мышление младшего школьника переживает переломный этап. Ещё недавно оно основывалось только на собственном опыте и ощущениях от окружающего мира. Но осваивая азы школьной программы, ребёнок учится не просто читать и писать, а соотносить символы со значениями и оперировать абстрактными единицами. Чтобы помочь ему освоится в мире букв и чисел, важно уделить внимание развитию логического мышления уже с 1 класса.

Прежде всего важно научить ребёнка наблюдательности: какими свойствами обладают те или иные предметы? Что в них общего? В чём различия? В процессе размышления над этим он получит представление о закономерностях, научится анализировать, сравнивать и обобщать.

Из классических настольных игр подойдёт домино. Эта игра учит быстро считать и принимать решения, предугадывая последствия. А также позволяет наглядно увидеть принцип логической цепочки.

Задачи на логическое мышление для 1 класса

Ответ: лиса, она обращена налево.

Ответ: чтобы узнать, какая цифра скрыта за грибком, решим пример «10-3». Ответ — 7. Решив пример «7+1», получим число, спрятанное за звёздочкой; это 8.

Развитие логического мышления во 2 классе

С 8-9 лет у ребёнка формируется критическое мышление: он больше не принимает на веру всё, что ему говорят. В этот период очень важно научиться отличать правду от неправды и сопоставлять данные из разных источников. В этом ребёнку помогут логические задачи на истинность и ложность суждений.

Игры в ассоциации, в слова и забавные «данетки» также очень хорошо развивают логику и воображение. А главная их прелесть в том, что играть можно где угодно, например, в транспорте или в очереди к врачу.

Кроме того, стоит познакомить ребёнка с задачками «с подвохом». Может показаться, что они носят исключительно шутливый характер, но это не так. С их помощью ребёнок научится понимать, что не все проблемы решаются стандартными методами.

Задачи на логическое мышление для 2 класса

Ответ: велосипед, он не жёлтый и без мотора.

Ответ: шесть, у пяти братьев одна общая сестра.

Развитие логического мышления в 3 классе

Знания ребёнка об окружающем мире становятся всё более глубокими и разносторонними. Он уже умеет соотносить разные пласты информации и строить гипотезы на основе имеющихся данных. Задания на поиск закономерностей по-прежнему актуальны, но теперь они должны быть гораздо сложнее.

Можно покупать более сложные головоломки, осваивать новые настольные игры. В этом возрасте многие дети увлекаются конструкторами. «Лего» и его аналоги помогают развивать логику, мелкую моторику и пространственное мышление, а главное, дают ребёнку огромное пространство для самовыражения.

Также в этом возрасте будут очень полезны математические и текстовые ребусы и занимательные игры со спичками.

Задачи на логическое мышление для 3 класса

Ответ:

Ответ: 4.

Развитие логического мышления в 4 классе

В 10-11 лет подростку хочется уже не просто играть, а сделать что-то по-настоящему. Это лучшее время для всевозможных экспериментов: опыты с переливанием жидкостей, электроконструкторы, развлечения с магнитами и кинетической энергией, химические реакции — всё это тоже отлично развивает логическое мышление. И конечно, пробуждает интерес к естественным наукам, которые скоро начнутся в школе. Не менее важно уделить внимание задачам на пространственное мышление, чтобы подготовиться к урокам черчения и геометрии.

А ещё в этом возрасте самое время познакомить подростка с основами программирования. Можно начать с изучения графического языка Scratch. Создавая с его помощью мультфильмы и простые игры, дети знакомятся с принципами работы системных алгоритмов.

Задачи на логическое мышление для 4 класса

Ответ: 30-9 = 21 — столько дополнительных выстрелов Вася заработал за попадания.

За каждое попадание давалось 3 выстрела: 21÷3 = 7 раз Вася попал по монстру.

Ответ: 2.

Резюме

Возможно, вас удивит, что ребёнок легко справляется с логическими задачами, которые казались вам трудными, и предлагает решения, о которых вы не подозревали. Дело в том, что детское мышление ещё не подвержено шаблонам и стереотипам. Важно помочь ребёнку сохранить эту пластичность ума. Чем раньше он начнёт развивать логику, тем легче ему будет учиться в дальнейшем.

В начальной школе «Фоксфорда» мы уделяем внимание логике с первого класса. Программа 1-4 классов включает курс алгоритмики, на котором дети учатся решать логические задачи, ребусы и головоломки, а в более старшем возрасте осваивают азы информатики и программирования. Такие занятия отлично развивают логическое мышление и позволяют овладеть навыками одной из самых востребованных профессий.

Пара советов напоследок:

Не ограничивайтесь только точными науками. Играйте с ребёнком в творческие игры: предложите нарисовать предмет по описанию его свойств, или составить рассказ, используя заданные словосочетания. Такие занятия не только тренируют логическое мышление, но и развивают фантазию и помогают ребёнку раскрыть творческий потенциал.
Не стоит заниматься развитием логики ребёнка слишком серьёзно. Лучше превратите занятия в игру. В будущем вашему сыну или дочери придётся решить немало по-настоящему серьёзных задач и находить выходы из непростых ситуаций. А пока пусть учится справляться с трудностями в игре.

Важность логического мышления на рабочем месте

Что такое логическое мышление и почему оно важно для работодателей? Слово «логика» происходит от греческого слова, означающего «разум». Работодатели высоко ценят работников, демонстрирующих сильное логическое мышление или умение рассуждать, потому что их решения основаны на фактических данных. В большинстве случаев организации не хотят, чтобы сотрудники принимали решения под влиянием эмоций, а не фактов.

Что такое логическое мышление?

Логические мыслители наблюдают и анализируют явления, реакции и обратную связь, а затем делают выводы на основе этих данных.Они могут обосновать свои стратегии, действия и решения на основе собранных фактов.

Логические мыслители не следуют своей интуиции и не разрабатывают стратегию, потому что она «кажется правильной». Логическое мышление также требует прояснения предположений и устранения предубеждений, насколько это возможно. Вот пример:

Торговый представитель изменяет презентацию продукта, чтобы подчеркнуть его удобство для пользователя, после получения отзывов от клиентов, указывающих на то, что простота использования была основной причиной того, что они приобрели продукт.

Расширять

Что такое дедуктивное рассуждение?

Логические мыслители также могут рассуждать дедуктивно. Они могут определить приемлемую предпосылку и применить ее к ситуациям, с которыми они сталкиваются на работе. Вот пример:

Организация может работать с основным убеждением, что сотрудники более продуктивны, если они контролируют способы выполнения своих обязанностей. Менеджер может продемонстрировать логическое мышление, используя дедуктивное мышление, встречаясь с подчиненными, сообщая о целях отдела и структурируя сеанс мозгового штурма для сотрудников, чтобы выбрать методы достижения этих целей.

Расширять

Важность логического мышления

Логическое мышление помогает всем сотрудникам обрабатывать факты и находить разумные решения, а не действовать исключительно на основе своих эмоций. Стратегия, основанная на логике, также может быть более убедительной для других сотрудников, чем стратегия, основанная на чувствах.

Примеры логического мышления

Ниже приведены некоторые примеры логического мышления на рабочем месте. Взгляните на этот список и подумайте о ситуациях на работе, в которых вы использовали логику и факты, а не чувства, чтобы работать над решением или установить курс действий.

Проведение маркетинговых исследований для оценки реакции потребителей на новый продукт перед разработкой рекламной стратегии.
Разработка профиля приема на работу новых торговых представителей на основе оценки качеств наиболее продуктивных торговых представителей компании.
Рекомендации стратегии отказа от курения после обзора последних обзорных исследований по отказу от курения.
Анализ отзывов посетителей ресторанов перед составлением протоколов обучения.
Опрос сотрудников об их предпочтениях в отношении вознаграждений сотрудникам до заключения контрактов с поставщиками.
Получение отзывов от пользователей об их опыте работы с программным обеспечением перед созданием следующего поколения.
Решение, кого назначить руководителем группы после сравнения прошлых свидетельств лидерского поведения потенциальных кандидатов.
Опрос увольняющихся сотрудников для выявления нежелательной текучести кадров.
Обращение к коллегам в других организациях, чтобы узнать о высокоэффективных методах, прежде чем доработать стратегию для следующего цикла.
Создание слоганов кампании на основе оценки горячих вопросов для потенциальных избирателей.
Подрядчик, рекомендующий дополнительную изоляцию, высокоэффективное отопительное, охлаждающее оборудование и приборы, а также конструкцию с пассивной солнечной батареей для клиента, который хочет максимально энергоэффективный дом.

Как продемонстрировать логическое мышление кандидату

Во время собеседования вы, скорее всего, не услышите вопрос, в котором прямо упоминается логическое мышление.То есть интервьюеры не скажут: «Приведите мне пример случая, когда вы использовали логику на работе». Вместо этого интервьюер может сказать: «Расскажите мне о шагах, которые вы предприняли для определения следующих этапов в упомянутом вами проекте». Или они могут спросить: «Как бы вы отреагировали, если новый выпущенный продукт получил отрицательные отзывы?»

В своих ответах на подобные вопросы вы хотите обрисовать в общих чертах шаги, которые вы предпримете для данного сценария.

Расскажите о процессе, который вы использовали бы для принятия решения, или расскажите о том, как вы устанавливали стратегию в прошлом.

Вы можете обсудить, какие вопросы вы задали, данные, которые вы использовали, или исследования, которые вы проанализировали, чтобы сделать выводы. Это поможет продемонстрировать ваши навыки логического мышления.

Вы также можете подчеркнуть способности логического мышления в своем резюме или сопроводительном письме. Опять же, вы просто хотите обрисовать свой процесс. Например, вместо того, чтобы просто сказать: «Создана новая программа обучения», вы можете добавить дополнительные сведения:

«Запрошены и проанализированы отзывы клиентов, а затем создана новая программа обучения сотрудников для устранения слабых мест и стандартизации работы сотрудников.«

Расширять

Напоминаем, что работодатели ищут кандидатов с опытом логического мышления, потому что это обеспечивает плавный процесс принятия решений.

Что такое логическое мышление и как его укрепить

Когда мы говорим, что что-то логично, на самом деле мы имеем в виду, что это имеет смысл. Навыки логического мышления — это способность сосредоточиться на поставленной задаче, следуя цепочке мыслительного процесса, связывая одно утверждение за другим, пока не будет найдено наиболее логичное заключение.

Хотя многие и не замечают, каждый из нас ежедневно сталкивается с проблемами, которые преодолеваются благодаря нашим способностям рассуждать. При расчете цен в супермаркете, просто чтобы проверить, можем ли мы получить все необходимое по более низкой цене, или пытаясь уместить все наши обязательства в один день, наша мыслящая машина крутит колеса, чтобы найти идеальное решение.

Однако, если вы потерялись на кассе, что ж, возможно, вам придется поработать над развитием логического мышления.

Разделение труда в нашем мозгу — левое полушарие больше вовлечено в логическое мышление

Мозг представляет собой сложную структуру, разделенную на два полушария — правое и левое.

Хотя районы взаимодействуют друг с другом, правда в том, что одна сторона всегда доминирует над другой. Что касается этого разделения, то у каждой стороны своя цель и особый стиль мышления. Например, правая сторона отвечает за эмоции и творчество, тогда как левая сторона обеспечивает контроль над миксом и обеспечивает логику, когда что-то кажется запутанным.

Однако правая сторона мечтания также может повлиять на процесс логического мышления. По мнению исследователей, производительность логических рассуждений модулируется эмоциональным состоянием. Что еще интереснее, большинство детей оцениваются как очень творческие, прежде чем пойти в школу с логической ориентацией. По крайней мере, так было раньше, поскольку школьная система теперь предлагает некоторые возможности для творческих занятий, таких как искусство и ремесла.

Левое полушарие мозга улучшает понимание математики и естественных наук, поскольку оно обрабатывает информацию от части к целому.Эти последовательности, скрытые в числах, символах и буквах, намного яснее, если они расположены в логическом порядке.

С другой стороны, правая сторона смотрит на все изображение только для того, чтобы разбить его на более мелкие части. Точно так же люди с правой стороны любят конкретные вещи, которые они могут обонять, почувствовать или попробовать, и им трудно выразить словами.

Логическая сторона левого полушария включает:

Логика;
Фактов;
Детали;
Паттернов;
Стратегии;
слов;
Язык;
Заказать;
Восприятие;
Прошлое и настоящее;
Практичность;
Безопасность;
Понимание;

Логическое мышление — это не врожденный талант, а то, чему можно научиться и практиковаться

Улучшение логического мышления — это просто научиться уделять больше внимания деталям.Поэтому есть несколько простых методов, которые помогут вам преодолеть препятствия в мышлении и действительно сосредоточиться.

Перестаньте смотреть на вещи только с вашей точки зрения

Для развития процесса логического мышления важно отличать установленные факты от личных наблюдений. Сосредоточение внимания на окружающей среде и своих чувствах — это всего лишь индивидуальное восприятие, которое не следует путать с логикой.

Например, предположим, что два человека собрались вместе, чтобы вместе поесть. Для одного блюдо пахнет отталкивающе, а другой наслаждается обедом.Первому человеку не понравился запах, поэтому они пришли к выводу, что еда несъедобная, нездоровая и неправильно приготовленная. Это нелогичный способ прийти к правильному выводу.

Во-первых, у человека А не было никаких подтверждающих доказательств того, что еда была нездоровой или плохо приготовленной. Следовательно, выводы, сделанные из этого наблюдения, неадекватны.

Чтобы прийти к логическому выводу, нужно отказаться от собственных искаженных мнений и сосредоточиться на проверенной информации, такой как ингредиенты, используемые для приготовления блюда, способы приготовления пищи и оборудование, используемое для ее приготовления, чтобы они могут составить четкое заявление.Помимо наблюдаемых фактов, вывод также должен быть сделан на основе кулинарных знаний, а не на основе расчетных предположений.

Подумайте, прежде чем приступить к делу — создайте стратегию

Поскольку логическое мышление предполагает замечать все детали и соединять их одну за другой, пока картина не станет ясной как день, стратегия играет важную роль в процессе мышления. Обучение стратегическому мышлению не только укрепит мозг, но и поможет вам быстрее и эффективнее справляться с деловыми обязательствами.А как развить такой полезный навык?

Начните с вопросов и попыток интерпретировать повторяющиеся модели. Учитесь на ошибках, чтобы предвидеть, что вас ждет впереди. Держите ум постоянно активным, ищите детали и узнавайте, как они действуют индивидуально и в группе, прежде чем сосредоточиться на более широкой картине.

Тщательно исследуйте значение слов

Поскольку логика более вербальна, небольшие языковые вариации имеют большое значение. Знание разницы между утверждениями определенно закрутил ослабленные гайки логического мышления.

Если вы слышите «необходимо» в заявлении, вы сразу понимаете, что есть условие, которое необходимо выполнить, в отличие от «достаточно», которое означает минимальный уровень усилий, которые приведут к положительному результату. Каждое условие имеет небольшое изменение значения, так же как порядок слов в предложении несет определенное значение.

Это не одно и то же, если кто-то говорит: «Если ты сделаешь это, то получишь награду» или «Если ты получил награду, то это произошло потому, что Я сказал тебе это сделать».Это может быть не обнаружено сначала, однако вариация все еще существует. В первом предложении есть условие, по которому человек получает вознаграждение, а во втором оно обратное, что означает, что оно противоречит первому утверждению и его заключению.

Развивайте свое логическое мышление в свободное время — Игры и мистические книги

Каждый день мы убегаем в цифровой мир в поисках новой формы развлечения. Но почему бы не использовать его для улучшения наших логических рассуждений? Математика не должна быть скучной, если ее использовать как игру.

В Интернете или в виде приложений есть множество умственных задач, которые улучшают нашу память и логическое мышление. Можно даже получить выгоду от игр в Facebook Poker. Карточные игры делают вас более сосредоточенными и аналитическими, следовательно, активируют левое полушарие мозга.

Кроме того, заблудиться в загадочной книге — это не только для правых. На самом деле, хорошая книга-головоломка может помочь вам работать над процессом стратегического мышления, решая все различные загадки внутри.То же самое и с шахматами.

Даже гении не родились всезнающими; они изучали, исследовали и работали над своими навыками логического мышления. Итак, используйте перечисленные выше простые методы в повседневной жизни, чтобы улучшить не только свое логическое мышление, но и общую продуктивность. Покорив поле логических рассуждений, никто больше никогда не сможет называть вас нереальным мечтателем.

Изображение предоставлено Волканом Ольмезом через unsplash.com

Логическое мышление — Edublox Online Tutor

Перед вами четыре блока: черный, красный, белый и зеленый.Вы должны удалить два из них. Вы не можете убирать красный, черный и белый блоки одновременно. Вы не можете убирать одновременно белый, зеленый и красный. Какие два блока можно убрать? Чтобы ответить на эту загадку, вам нужно будет мыслить логически.

Логическое мышление — это процесс, в котором человек последовательно использует рассуждения, чтобы прийти к заключению. Проблемы или ситуации, связанные с логическим мышлением, требуют структуры, отношений между фактами и цепочек рассуждений, которые «имеют смысл.”

В своей книге Создание мозга доктор Карл Альбрехт говорит, что в основе всего логического мышления лежит последовательное мышление . Этот процесс включает в себя принятие важных идей, фактов и выводов, связанных с проблемой, и их систематизацию в виде цепочки, которая сама по себе приобретает смысл. Думать логически — значит думать пошагово.

Навыки логического мышления дают учащимся возможность понять, что они прочитали или показали, а также использовать эти знания без дополнительных указаний.Логическое мышление учит студентов, что знания изменчивы и основываются на себе.

Логическое мышление также является важным основополагающим навыком математики. «Изучение математики — это очень последовательный процесс», — говорит д-р Альбрехт. «Если вы не усвоите определенную концепцию, факт или процедуру, вы никогда не сможете надеяться понять другие, которые появятся позже и зависят от них. Например, чтобы понять дроби, вы должны сначала понять деление. Чтобы понять простые алгебраические уравнения, необходимо знать дроби.Решение проблем со словами зависит от знания того, как составлять уравнения и манипулировать ими, и так далее ».

Логическое мышление — это не магический процесс или вопрос генетической одаренности, а усвоенный умственный процесс. Обучение логическому мышлению побуждает учащихся думать самостоятельно, ставить под сомнение гипотезы, разрабатывать альтернативные гипотезы и проверять эти гипотезы на основе известных фактов.

Доказано, что специальное обучение процессам логического мышления может сделать людей «умнее». Логическое мышление позволяет ребенку отвергать быстрые ответы, такие как «я не знаю» или «это слишком сложно», давая ему возможность глубже вникнуть в свои мыслительные процессы и лучше понять методы, используемые для нахождения решения, и даже само решение.

Помимо еды, воды и крова, единственное, что человеку больше всего понадобится в жизни, — это образование. Из этих четырех потребностей образование — единственное, что может помочь обеспечить постоянную способность человека обеспечивать себя тремя другими. К сожалению, важность навыков логического мышления в образовании недооценивается, и поэтому обучение навыкам логического мышления сильно игнорируется.
.

простых способов улучшить логическое мышление

Вы видели новое телешоу «Шерлок», на этот раз в роли талантливого Бенедикта Камбербэтча? Если да, то вы, вероятно, завидуете его удивительным навыкам дедукции и задаетесь вопросом: «Как он это делает?» Правда в том, что вы тоже можете это сделать.

Что ж, может быть, вы не можете раскрыть сложное дело об убийстве, но вы можете улучшить свое логическое мышление с целью облегчить решение проблем и принятие решений. В свою очередь, эти навыки будут способствовать вашему успеху в работе и в жизни в целом.

Вот несколько приемов и упражнений, которые помогут вам отточить свой ум.

Делаем логические выводы

Хотя вам это может показаться глупым, старайтесь мыслить условными утверждениями и находить причины и следствия небольших и, возможно, незначительных фактов.Например, предположим, что каждый раз, когда идет снег, на улице холодно. В предложении говорилось: «Если идет снег, на улице холодно».

В условных предложениях, если посылка (первая часть предложения) верна, то верным будет и заключение (вторая часть). Попробуйте сделать то же самое с другими вещами (если я уроню свой телефон, он будет испорчен; если я не буду есть, я буду голоден и т. Д.), И посмотрите, работает ли эта взаимосвязь посылки и заключения наоборот. .

Играть в карточные игры

Кто сказал, что оттачивание логического мышления должно быть скучным? Напротив. Раз в неделю собирайте друзей и играйте в карточные игры, которые стимулируют ваш мозг думать быстро и логично. Сложные карточные игры не только полезны для души и занимательны, но и улучшают вашу память, концентрацию внимания и аналитические способности.

Если вы включите стратегию в эту смесь, они станут еще лучше. Дети могут поиграть в веселые игры Crazy Eight или Go Fish, а взрослые — поиграть в блэкджек или покер.

Занимайтесь математикой

Нет сомнений в том, что математика — одно из лучших упражнений для улучшения логических навыков. Тем не менее, это может быть действительно непривлекательным занятием как для детей, так и для взрослых. К счастью для вас, есть много интересных способов поработать над своей математикой. И взрослые, и дети могут найти удовольствие и интеллектуальные задачи в математических играх на различных веб-сайтах или с помощью приложений для смартфонов.

Судоку и другие игры, включающие веселую и увлекательную работу с числами, в конечном итоге могут улучшить способность мозга быстрее решать реальные задачи.

Разгадайте тайны и взломайте коды

Чтение детективных рассказов и детективов требует от читателей логического мышления. Вы можете получить аналогичный опыт, просмотрев такие фильмы или телешоу. Попробуйте разгадать какую-нибудь загадку раньше, чем это сделает герой рассказа.

Не расстраивайтесь, если все идет не так, как вы себе представляли. Просто вспомните слова знаменитого героя из начала этой статьи: «Когда вы устранили невозможное, все, что остается, каким бы невероятным оно ни было, должно быть правдой.«Так что устраните невозможное и невероятное, и решение придет к вам. Коды взлома (созданные вашими друзьями или найденные в Интернете) — еще одно отличное упражнение для мозга.

Провести дебаты

Вы когда-нибудь вступали в спор, когда не могли найти правильных аргументов, чтобы объяснить, почему что-то хорошо или плохо? У всех есть. Дебаты — это здорово, потому что они побуждают вас искать причины и следствия, превращать их в твердые аргументы и находить за всем этим логику.

Поскольку дебаты требуют логического мышления и принятия решений на ходу, они могут обострить ваш разум. Итак, вы можете присоединиться к дискуссионному клубу или организовать дебаты с друзьями о политике, музыке, обществе, литературе и т. Д.

Будьте стратегом

Поскольку логическое мышление — это соединение частей, стратегическое мышление играет важную роль в этом процессе. Стратегическое мышление не только зарядит ваш мозг энергией, но и станет полезным активом для принятия решений, связанных с работой, и даже для успеха в личной жизни.

Вот некоторые из основных привычек, которые вам следует приобрести для этой цели: предвидение (думать о том, что впереди), критическое мышление (подвергать сомнению все), интерпретация (поиск шаблонов), принятие решений (приход к выводу) и обучение (на своих ошибках). . Оттачивайте свое стратегическое мышление, играя в стратегические игры (настольные игры, карточные игры, видеоигры и т. Д.) И разрабатывая стратегию для спортивных мероприятий.

Так же, как важно найти свой внутренний баланс и работать над своей духовностью, так же важно поддерживать свой мозг постоянно активным с помощью сложных игр и задач, чтобы вы улучшили свой логический интеллект, который имеет решающее значение для успеха и, следовательно, , гармоничная жизнь.Воспользуйтесь советами, которые мы вам дали, и довольно скоро вы откроете для себя своего внутреннего Шерлока Холмса.

Безопасность | Стеклянная дверь

Мы получаем подозрительную активность от вас или кого-то, кто пользуется вашей интернет-сетью. Подождите, пока мы подтвердим, что вы настоящий человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, напишите нам чтобы сообщить нам, что у вас возникли проблемы.

Nous aider à garder Glassdoor sécurisée

Nous avons reçu des activités suspectes venant de quelqu’un utilisant votre réseau internet.Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un электронная почта à pour nous informer du désagrément.

Unterstützen Sie uns beim Schutz von Glassdoor

Wir haben einige verdächtige Aktivitäten von Ihnen oder von jemandem, der in ihrem Интернет-Netzwerk angemeldet ist, festgestellt. Bitte warten Sie, während wir überprüfen, ob Sie ein Mensch und kein Bot sind.Ihr Inhalt wird в Kürze angezeigt. Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте: .

We hebben verdachte activiteiten waargenomen op Glassdoor van iemand of iemand die uw internet netwerk deelt. Een momentje geduld totdat, мы узнали, что u daadwerkelijk een persoon bent. Uw bijdrage zal spoedig te zien zijn. Als u deze melding blijft zien, электронная почта: om ons te laten weten dat uw проблема zich nog steeds voordoet.

Hemos estado detectando actividad sospechosa tuya o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para informarnos de que tienes problemas.

Hemos estado percibiendo actividad sospechosa de ti o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real.Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para hacernos saber que estás teniendo problemas.

Temos Recebido algumas atividades suspeitas de voiceê ou de alguém que esteja usando a mesma rede. Aguarde enquanto confirmamos que Você é Uma Pessoa de Verdade. Сеу контексто апаресера эм бреве. Caso продолжить Recebendo esta mensagem, envie um email para пункт нет informar sobre o проблема.

Abbiamo notato alcune attività sospette da parte tua o di una persona che condivide la tua rete Internet.Attendi mentre verifichiamo Che sei una persona reale. Il tuo contenuto verrà visualizzato a breve. Secontini visualizzare questo messaggio, invia un’e-mail all’indirizzo per informarci del проблема.

Пожалуйста, включите куки и перезагрузите страницу.

Это автоматический процесс. Ваш браузер в ближайшее время перенаправит вас на запрошенный контент.

Подождите до 5 секунд…

Перенаправление…

Код объявления: CF-102 / 67677dfabdc03a7d.

Как мыслить логически (и постоянно решать серьезные проблемы)

Подкаст: Скачать

Подписка: Apple Podcasts | Подкасты Google | Брошюровщик | RSS

Если вы хотите с легкостью решать жизненные проблемы, вы должны научиться мыслить логически, верно?

Да, но не так быстро.

Вы хотите убедиться, что используете правильных типов логики для решения текущих задач.

Видите ли, логические мыслители делают то, что делаю я сейчас:

Они ставят паузу на такие вопросы и начинают их раскручивать.

Почему? Потому что сама логика часто включает копания глубже, и анализ различных точек зрения.

Например, одна из форм логического мышления, которую вы скоро обнаружите, заставит вас немедленно спросить…

Существует ли несколько логических схем для быстрого решения жизненных проблем? Или я могу изучить альтернативы вне логики?

Логический мыслитель может сделать то же самое с самой идеей «проблемы».

Это делается путем «мысленного вращения» обсуждаемой темы и наблюдения за тем, что на самом деле это может вообще не быть проблемой.

Это может быть путь к решению.

Yours Free: частный курс со шпаргалками для того, чтобы стать мастером запоминания, начиная с нуля.

>>> Нажмите здесь, чтобы увидеть специальное бесплатное предложение .

Как мыслить логически: 9 способов улучшить свои навыки логического мышления

В конце концов, использование правильной формы логики — это скорее наилучшее возможное решение, чем проблема, но нам нужно сначала убедиться, что мы понимаем проблему.

Если вы слышали, как Илон Маск говорил об основных принципах мышления, то это форма логики, которую он использует, чтобы помочь людям процветать на далеких планетах после смерти Земли. И лучше общаться здесь, на нашей драгоценной планете, пока мы еще можем.

Это реальные проблемы, и необходимы правильные формы логики.

Лучшая часть?

Существует намного больше способов логического мышления для решения глобальных и личных проблем, так что приступим.

One: погрузитесь в логическое мышление

Улучшение логических рассуждений начинается с знания типов логики, имеющихся в вашем распоряжении.

Изучение истории логики стоит вашего времени, потому что это поможет вам увидеть, как люди открыли эти принципы и со временем усовершенствовали их на практике.

Как вы скоро обнаружите, многие культуры определили и использовали логические формы, такие как:

Философская логика
Неформальная логика
Формальная логика
Модальная логика
Математическая логика
паранепротиворечивая логика
Семантическая логика
Логика вывода
Систематическая логика

В связи с этим у вас есть разница между тем, что философ Элайджа Миллграм называет теоретическим рассуждением, ипрактическое рассуждение. Первый включает выяснение фактов, второй — процесс определения того, какие действия следует предпринять на основе того, что в идеале является набором точных фактов.

Итак, обычно люди, которые хотят мыслить более логично, на самом деле стремятся к первой категории или философской логике. Это также называется «рассуждением» и включает в себя навыки:

Вычет
Индукция
Причинный вывод
Аналогия

Дедуктивное мышление — это то, о чем мы думаем, когда думаем о Шерлоке Холмсе, который строит свои доводы, аргументируя общие принципы.Он использует их, чтобы описывать определенную серию событий и разгадывать различные загадки.

Индуктивное мышление по существу является обратным этому процессу. Вместо того, чтобы использовать общие принципы для уточнения деталей, вы используете конкретные детали для обобщения. Например, вы могли заметить, что я публикую в этом блоге почти каждую неделю и использую индуктивные рассуждения, чтобы логически определить, что я постоянный блогер.

Причинно-следственный вывод помогает понять научную причину, почему и как все меняется.Например, почему вы читаете эту статью? Я могу логически сделать вывод, что это потому, что вы хотите испытать изменения и стать лучше мыслителем.

(Или, может быть, вы хотите испытать больше, например, все эти 11 преимуществ критического мышления.)

Рассуждения по аналогии или аналогии включают сравнения, основанные на установленных примерах или моделях.

Например, мы знаем, что почти каждый поборник памяти открыто признает, что у них есть нормальная память, которая не работает особенно хорошо без использования мнемонических устройств.По аналогии мы можем сделать вывод, что любой человек со средними способностями памяти может стать чемпионом по памяти.

Как долго нужно изучать логику? Я бы посоветовал по крайней мере 90 дней, чтобы вы могли получить обзор с высоты птичьего полета и достаточно подробных деталей.

Логические мыслители всегда следят за тем, чтобы у них был вид с высоты птичьего полета и в то же время мелкие детали.

Кроме того, как вы скоро обнаружите на этой странице, есть и другие поля, из которых вы можете читать, чтобы улучшить свое логическое мышление.

Два: глубокое понимание проблем, которые вы пытаетесь решить

Вы когда-нибудь проходили викторину и понимали, что ответили, прежде чем задумались над вопросом? Вы могли понять это правильно, но ваши импульсы взяли верх, и вы потеряли драгоценные очки.

Дело не в том, что вы были нелогичны. Вы просто не нашли времени, чтобы полностью понять вопрос, и причина, по которой вы этого не сделали, могла быть логичной. Например, с одной точки зрения, в некоторых случаях было бы совершенно логично торопиться с экзаменом, если у вас не хватает времени.

Но в целом мы хотим быть уверены, что глубоко понимаем проблемы, с которыми сталкиваемся. Вот почему Авраам Линкольн сказал знаменитую фразу:

«Дайте мне шесть часов, чтобы срубить дерево, и я потрачу первые четыре часа на то, чтобы точить топор».

Линкольн использует здесь аналогию, в которой «топор» выступает в качестве аналогии. Это говорит о том, что нужно потратить время на то, чтобы убедиться, что вы используете правильные инструменты для работы. Более того, прежде чем использовать их, убедитесь, что они в отличной форме.

Еще одна причина узнать больше о различных формах логики. Это поместит больше инструментов в ваш ящик для инструментов и позволит вам поддерживать их остроту.

Вот еще 9 стратегий критического мышления, которые помогут вам оставаться острым.

Три: дополнительные сведения о языке

Многим людям сложно мыслить логически, потому что они недостаточно понимают, что означают слова.

Логическое мышление включает нюансы, поэтому чем больше вы знаете о словах и их значениях, тем более точным умом вы будете принимать решения.

Вот как запоминать словарный запас для совершенствования. Это поможет вам добавить больше значений к словам и добавить больше определений к тем, которые вы уже знаете. Вам также поможет изучение происхождения слов и того, как работают префиксы и суффиксы.

Помимо изучения слов и их значений, поможет изучение языка и логики, например изучение силлогизмов и логических ошибок.

Бонусный совет:

Погрузитесь глубже и узнайте как можно больше о заблуждениях, чтобы вы действительно знали свое дело.Если вы этого не сделаете, легко попасть в ловушку мышления.

Например, некоторые люди любят обвинять других в заблуждении о скользком пути, не осознавая, что на самом деле существует шесть видов этого заблуждения.

Если вы хотите мыслить логически, стоит быть внимательным. Вот почему в следующий раз мы сосредоточимся на тщательности.

Четыре: быстрое чтение без ущерба для тщательности

Улучшение словарного запаса имеет огромное значение для улучшения логического мышления и поможет вам быстрее читать.

Но чтобы со временем улучшить свои логические навыки, вам нужно внимательно читать.

Я предлагаю вам читать книги побольше и больше, начиная с основных учебников в интересующей вас области.

Выбирая самые крупные и авторитетные книги, вы будете читать более логично.

Создание основ в своем уме путем чтения авторитетных учебников поможет вам развить распознавание образов. Этот навык приводит к более быстрому использованию логических форм вывода, которые мы обсуждали в первой части этой статьи.

Пять: прослушивание длинного содержимого

Краткое содержание заставляет людей делать поспешные суждения и перебивать людей до того, как они услышат всю историю. Логические мыслители защищают себя, практикуя слушание в течение длительных периодов времени.

Не только полезно читать длинные книги, но и вы научитесь думать гораздо более логично, если будете слушать, как логичные люди думают вслух.

Дебаты — отличный способ сделать это, и Интернет позволяет найти многие из них.

Однако важно обращать внимание на обе стороны аргумента.

Слушая, тренируйтесь думать о себе, мысленно репетируя доказательства, которые вы могли бы предоставить в поддержку своих взглядов. Также подумайте, как бы вы отреагировали.

Еще один совет:

Обратите внимание на пробелы в аргументах, предложенных участниками дебатов, и перечислите способы, которыми вы могли бы восполнить пробелы.

И если вы хотите вспомнить больше о том, что происходит во время дебатов, вам поможет Мастерство Дворца памяти.

Шесть: Расширьте свой кругозор с помощью нескольких носителей

Я только что предложил вам попробовать «подумать вслух» и смоделировать это самостоятельно.

Но вы захотите выйти за рамки логических упражнений в уме. Вам также следует:

Чтобы попрактиковаться в логической речи, участвуйте в как можно большем количестве дискуссий о реальных проблемах. Конечно, есть место для разговоров о фильмах и спорте. Но если вы хотите научиться мыслить более логично, вам нужно практиковать это самостоятельно в реальном времени.

Письмо всегда является ключом к развитию логического мышления, поэтому я предлагаю вам вести дневник. Эта простая практика поможет вам увидеть собственный мыслительный процесс и со временем улучшить его.

В совокупности у вас будет много возможностей для самоанализа. Если вы можете записывать свои разговоры и просматривать их расшифровки, тем лучше.

Семь: задавайте лучшие вопросы

Многие из нас задают типичные вопросы W5 и на этом останавливаются:

Кто
Что
Где
Когда
Почему
Как

Но чтобы практиковать логическое мышление, вы хотите выйти за рамки этих вопросов.Задайте дополнительно к этим вопросам:

По кому?
По какому прецеденту?
Где это не так?
Когда это было не так?
Почему именно сейчас?

Есть много вариантов этих вопросов, которые вы можете задать, и я расскажу больше об этом в сообщении нашего сообщества о том, как думать быстрее.

Восемь: Изучите теорию игр

Один из малоизвестных способов научиться логическому мышлению — это изучение игр и метаигр.

Короче говоря, теория игр изучает области конкуренции, в которых люди регулярно принимают решения. На эти решения влияют другие люди в этом районе и, в свою очередь, влияют на других.

Моделируя способы взаимодействия людей в конкурентной среде, вы можете научиться мыслить более логично и избегать когнитивных предубеждений, которые вредят вашей жизнедеятельности.

Вам понравится избегать многих проблем, потому что теория игр помогает научить ваш разум предвидеть возможные результаты различных решений.Заранее продумав последствия, вы избавите себя от многих неприятностей.

Примечание: вы также можете применить теорию игр к прошлому, подумав о том, что бы произошло, если бы люди действовали иначе. Это называется проработкой контрфактов исторической ситуации и может быть использовано в вашей личной жизни и в больших группах.

Некоторые люди думают, что теория игр имеет ограниченное значение для повседневной жизни, но я не думаю, что они… логичны в этом отношении.Мы все оказываемся в ситуациях, когда на нас влияют определенные действия, и понимание этого давления поможет вам лучше реагировать.

Ключевой пример — использование задачи Монти Холла или задачи трех дверей для принятия решений.

Логические упражнения, такие как Задача Монти Холла, помогут вам продумать, что делать, когда вы сталкиваетесь с выбором в жизни.

Некоторые спорят о том, действительно ли логично использовать эту проблему в жизни, но я могу подтвердить ее ценность.

Например, когда я вижу возможность сделать что-то другое и чувствую, что хочу по умолчанию вернуться к своим предыдущим решениям, я вспоминаю этот теоретический пример игры и напоминаю себе, что нужно пройти «менее пройденный путь».

Математика на моей стороне?

Думаю, да, потому что я побывал во многих приключениях, которые, как подсказывает логика, не могло бы случиться, если бы я решил придерживаться того же самого.

Чтобы узнать больше об этих ситуациях, ознакомьтесь с историями, которые я рассказываю в книге «Победоносный разум: как овладеть памятью, медитацией и психическим благополучием».

Девять: правила использования и ограничения

Я не любил правила. В некотором смысле я до сих пор этого не делаю.

Но однажды я наслаждался ужином с Тони Бьюзеном, экспертом по памяти, новатором ментальных карт и соучредителем чемпионата мира по запоминанию.

Я рассказал ему о том, как иногда переключаю системы памяти во время испытаний на время для чисел и игральных карт.

Он сказал: «Правила сделают тебя свободным».

Тони Бьюзен с Энтони Метивье и Филом Чемберсом

Это важно, потому что жизнь, как и тренировка памяти, часто дает нам возможность использовать несколько техник.

Например, при запоминании чисел мы могли бы выбрать систему Доминика или основную систему, хотя, как я обнаружил, не стоит переключаться с одной на другую во время гонок на время.

Но, желая ограничить себя и придерживаться «правил» только одной системы, мы можем улучшить нашу производительность.

Это верно и в жизни, где вы можете изучить определенные практические правила и придерживаться их.

Возьмем другой пример, изучив логику У. Чипа и Дэна Хита.РЭП. техника и практика ее в течение долгого времени были чрезвычайно полезны для меня.

На самом деле, это настолько полезно, что «нелогично» забывать не использовать его при принятии решений. Вот почему я запомнил его с помощью специальной техники запоминания, называемой ars combinatoria, что было очень важно в истории развития логического мышления.

Какие практические правила, которые помогут вам «ограничить» себя продуктивной формой мышления и принятия решений, вы можете принять?

Логическое мышление — это вознаграждающий процесс, которым нужно наслаждаться на всю жизнь

Вам понравилось изучать эти девять способов улучшить свое логическое мышление?

Я надеюсь на это, и надеюсь, что вы сделаете практику некоторых из этих подходов своим личным хобби.

Вы можете легко практиковать логическое мышление во время медитации или работы с альтернативой логике, такой как дзен.

В качестве заключительного совета, для меня было бы логичным порекомендовать противоположное логике.

Видите ли, есть практики, подобные Дзен, которые эволюционировали, чтобы помочь нам увидеть и испытать пределы логики. Дзен обращает язык против самого себя, чтобы помочь нам испытать душевное облегчение от проблем, о которых мы так много думаем.

Одна из лучших книг, помещающих эту тему в более широкую сферу вычислительного мышления как для людей, так и для машин, — это Gödel Escher Bach .Интересным источником для коллекции коанов является The Gateless Gate от Mumon.

Я говорю об обратном логике не только потому, что это логично. Чтобы в полной мере ощутить преимущества логического мышления, вам нужно уметь вообще выйти за рамки мышления.

Недостаточно глубоко задавать вопросы. Нам нужно подвергнуть сомнению сам процесс вопрошания как привычку к обучению на протяжении всей жизни.

Итак, давайте начнем допрос. Дайте мне знать, какой из этих способов улучшить свое мышление вы собираетесь попробовать и какие вопросы по логике у вас еще остались?

Yours Free: частный курс со шпаргалками для того, чтобы стать мастером запоминания, начиная с нуля.

>>> Нажмите здесь, чтобы увидеть специальное бесплатное предложение .

возрастов и этапов: помощь детям в развитии навыков логики и рассуждения

От 3 до 4 Это имеет для меня смысл! Сьюзен А. Миллер, изд.

Трехлетний Скотт настаивает на том, что его высокая куча блоков содержит больше, чем ровный ряд блоков Рошель, даже после того, как его учитель помогает ему считать каждую группу. Скотт все еще использует наблюдения, чтобы сказать ему, что в его «большой» стопке больше.Скотту потребуется больше опыта с участием учителя и скачок в развитии, чтобы понять, что его первоначальное восприятие было неверным.

Дошкольники на предоперационной стадии развития используют свое восприятие окружающей среды вместе с фрагментами информации, собранной во время их прошлого опыта, чтобы понять свой мир. Они основывают свое понимание на том, что видят, а не на логике. Им нужно пройти через множество нелогичных мыслительных процессов, прежде чем они смогут даже начать логически осмыслять свой мир.

Обучение методом проб и ошибок

Предоставляя детям возможность учиться через игру, помните о следующих характеристиках их мышления:

Вт

Судя по внешнему виду. Когда форма или внешний вид материала меняются, дошкольникам трудно понять, что количества остаются прежними (или «сохраняются»). Например, во время перекуса Джанель бросает на стол коробку с крекерами.Латиса заглядывает в свою плотно заполненную коробку с крекерами, затем надувается и спрашивает, почему у Джанель еще крекеров. Она не понимает логически, что, если бы крекеры Джанель были помещены обратно в коробку, количество было бы таким же.

Глядя на одну вещь за раз. Поскольку дошкольникам трудно сосредоточиться не только на собственном единственном восприятии, они склонны сортировать предметы по одной характеристике, а не по двум. Например, если дать несколько небольших блоков разного размера, цвета и формы, молодые троицы могут решить отсортировать их, выровняв их по размеру и назвав «парадом».«Однако более старые тройки и четверки могут упорядочить их по двум атрибутам (сначала по цвету, а затем также по форме или размеру).

Не зная номеров. Дошкольники тоже довольно нелогичны, когда дело касается числовых концепций. Поскольку Чарли наливает ведра воды и повторяет наизусть «четыре, пять, шесть», его счет может совсем не соответствовать количеству, которое он наливает. Опять же, именно через конкретный опыт он придет к пониманию значения чисел и счета.

Что вы можете сделать

Учитывать разные стили обучения. Некоторым детям нравится прыгать и бездельничать. Предоставьте этим детям множество открытых материалов для изучения. Другим детям удобнее наблюдать за игрой и задавать вопросы. Убедитесь, что у них достаточно времени, чтобы обсудить происходящее.

Развивайте у детей любопытство и мыслительные способности. Предложите ряд интригующих манипуляторов. Например, попросите детей сравнить цветные стержни по размеру и нанизать бусинки для создания узоров. Укажите на причинно-следственные связи.Когда они добавляют яйцо в муку во время кулинарных экспериментов, спросите: «Что может случиться дальше?» Используйте открытые вопросы для поддержки оценки и прогнозирования.

Предлагайте задачи мышления в течение дня. Когда дети откладывают кубики и книги во время уборки, поощряйте их классифицировать предметы. Предложите им сравнить количества, играя в продуктовом магазине в классе.

от 5 до 6 Измерьте это так! , автор — Эллен Бут Черч,

«Миссис Миллс, вы знали, что на этом столе восемь книг, а в книжном шкафу девять? У меня семь книг, а Натану шесть.Сколько у вас книг? Может быть, 10! »

В этом детском саду практический опыт, подобный этому, естественным образом ведет к развитию абстрактного мышления и навыков обработки. Эти 5- и 6-летние дети экспериментировали с использованием книг в качестве единицы измерения. По мере того, как они свободно и открыто исследовали концепцию нестандартных измерений, они начали понимать применение теории и возможности ее использования. Они наблюдали сходства и различия между объектами, которые они измеряли.И хотя книги, которыми они использовали для измерения, были далеки от стандартного размера, дети устанавливали абстрактную связь между измеряемым объектом и инструментом, который они использовали.

На этом этапе дети развивают способность удерживать информацию в уме, а затем использовать ее для сравнений. Процесс этих сравнений — важный шаг в абстрактном мышлении. Например, осенью этот класс использовал яблоки как нестандартную единицу измерения и вспомнил, что их учитель был длиннее, чем они.Они не помнили, сколько еще осталось, но они осознали, что 10 книг — это больше, чем семь — применяя эту концепцию тогда и позже, — а это действительно абстрактное мышление в действии!

Это имеет смысл!

В процессе развития дети 5 и 6 лет балансируют между конкретным и абстрактным опытом. Они не готовы учиться всему на бумаге, карандаше и механических задачах, но способны видеть связь между конкретным опытом и абстрактным представлением.Подсчет количества книг и представление этой информации на диаграмме или графике с помощью наклеек или меток — ключевой навык — запись конкретного опыта в изобразительном или символическом виде. Это начало составления таблиц, записи и даже будущих заметок.

Поскольку их записи основаны на личном практическом опыте, дети в возрасте 5 и 6 лет также могут обращаться к своим таблицам и «читать» то, что они узнали. Их простые символы и изображения сродни алфавиту и чтению.Исследования показали, что когда воспитанники создают свои собственные абстрактные символические записи, они переходят к чтению с большей легкостью и пониманием.

Что вы можете сделать

Классы, наполненные учебой, наполнены активными действиями и открытыми вопросами. Предоставьте детям возможность работать с бетонными материалами. Если дети экспериментировали с наполнением водой контейнеров разного размера, предложите им попробовать еще раз с песком, счетчиками и мелками.

Предложите детям сравнить практических занятий. Диаграммы, графики и полевые книги могут служить мостом между конкретным и абстрактным.

Поощряйте детей делать прогнозы на основе предыдущего опыта.