Что такое конгруэнтность, или чем вредны хорошие манеры — T&P
«Теории и практики» продолжают объяснять смысл часто употребляемых выражений, которые зачастую используются в разговорной речи в абсолютно неправильном значении. В очередном выпуске рубрики — что думал Ларошфуко о дураках, в чем опасность неправильных подарков и почему пикапер должен быть конгруэнтным.
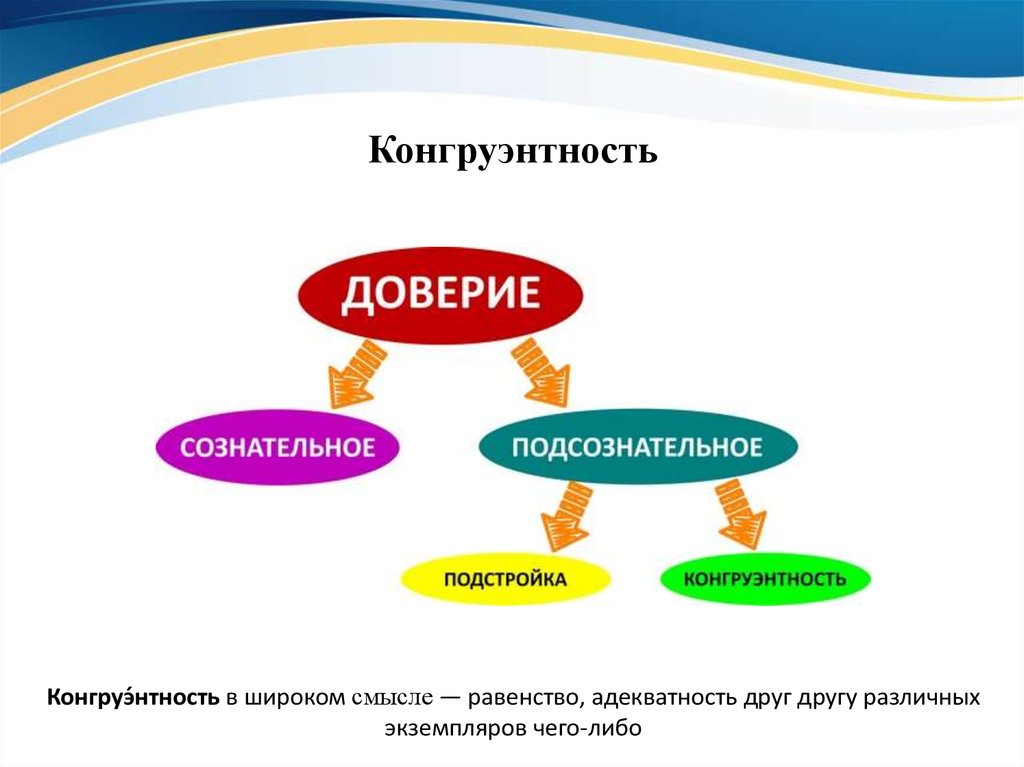
«Конгруэнтность» — слово, которое мы знаем из школьной программы по геометрии. Геометрические фигуры (или тела) конгруэнтны, если одна из них может быть переведена в другую с помощью движения — сдвига, вращения или зеркального отображения. Но, закончив школу, мы узнаем, что этот термин может иметь и другие значения, в том числе и в сфере человеческих отношений. Попробуем в них разобраться.
Латинское слово congruō означает «я совпадаю, я соглашаюсь». И в естественных науках, как и в точных, конгруэнтность означает эквивалентность предметов друг другу. Но перейдя в гуманитарные науки буквальное «совпадение» начинает приобретать новое, метафорическое значение.
Так появилось психологическое определение конгруэнтности.
Эту закономерность сформулировал еще Ларошфуко: «Стоит дураку нас похвалить, как он уже не кажется так глуп».
Его история началась в 1955 году, когда была опубликована «Теория конгруэнтности» американских психологов Осгуда и Танненбаума. Основной ее тезис заключался в том, что для того, чтобы побороть когнитивный диссонанс (конфликт идей и представлений в сознании индивида), человек одновременно изменяет свое отношение к двум противоречивым источникам информации.
Например, у вас есть приятель N, к которому вы прекрасно относитесь и считаете его умным и хорошим человеком. И тут он хвалит какое-то явление, которое вам совершенно не нравится — например, новый законопроект. Это создает противоречие: вы привыкли позитивно оценивать суждения N, но его позиция перестала совпадать с вашей. Чтобы восстановить гармонию, можно решить, что а) N дурак и вы в нем разочаровались б) N умный, а вашу позицию надо пересмотреть в) N в чем-то ошибается, но и ваша позиция не так уж правильна.
Последний вариант — лучший способ гармонично восстановить баланс оценок, который авторы теории и назвали конгруэнтностью.
Этот пример работает и в обратную сторону — допустим, вам неприятен какой-то человек и вдруг случайно обнаруживается, что он сходит с ума по вашему любимому художнику или высоко оценивает ваши достижения. И вроде он уже не так неприятен, не правда ли? Эту закономерность сформулировал еще в XVII веке писатель Франсуа де Ларошфуко: «Стоит дураку нас похвалить, как он уже не кажется так глуп».
Другой американский психолог Карл Роджерс разработал теорию личности, в которой понятие конгруэнтности имеет совсем иной смысл, чем в социальной психологии. Для него «конгруэнтность»— «термин, который мы используем для обозначения точного соответствия нашего опыта (переживания) и его осознания».
И снова приведем пример. Представим себе, что вы выясняете отношения с близким человеком и чувствуете явное раздражение и гнев, который вы неспособны скрыть. Но поскольку стать субъективным и «потерять лицо», поддаваясь эмоциям, означает проявить слабость, вы не хотите признавать свою злость и продолжаете верить в то, что всего лишь логично отстаиваете свою точку зрения.
В такой момент вы неконгруэнтны — вы потеряли соответствие переживания, его осознания и выражения.
Занятно, что из психологии конгруэнтность перекочевала в НЛП, а оттуда — в теории пикаперов. Разработчики планов покорения женщин уверены, что конгруэнтность — необходимое качество для уверенного в себе альфа-самца.
Или, допустим, вы мечтали получить на день рождения самокат, а друзья неожиданно вручают вам набор для покера. Вы не хотите расстраивать друзей и, кисло улыбаясь, благодарите за замечательный подарок. В данном случае вы понимаете, что чувствуете, но не можете это выразить — неконгруэнтность налицо.
И тут возникает серьезное противоречие между этикой и психологией. Роджерс считал, что конгруэнтность — залог внутренней гармонии личности: человек ничего в себе не подавляет, ни в чем себя не обманывает, а значит, становится самим собой и лучше понимает свои желания. С другой стороны, если мы начнем выражать все, что думаем и ощущаем, мы доставим много дискомфорта окружающим и наверняка нарушим ряд светских условностей.
И точку баланса тут каждый выбирает сам.
Занятно, что из психологии конгруэнтность перекочевала в НЛП, а оттуда — в теории пикаперов. Разработчики планов покорения женщин уверены, что конгруэнтность — необходимое качество для уверенного в себе альфа-самца. Но, в отличие от теории Роджерса просто быть собой тут все-таки недостаточно для счастья.
« Если вы слабак, и неинтересная серая мышь, то вы можете быть суперконгруэнтным, демонстрируя кто вы есть, но вы не будете клевым» — говорится в одном из пикаперских руководств. — Если вы клевый, но не конгруэнтный — значит вы слишком стараетесь (пытаетесь быть тем, кем в действительности вы не являетесь). Снова мимо. Для того, что бы вас считали привлекательным, вы должны обладать обеими характеристиками». Надо отдать должное автору — определенная логика в этом есть.
Как говорить
Неправильно: «Почему ты на меня кричишь? Что за неконгруэнтная реакция?». Правильно: «неадекватная»
Правильно: «Тебе надо стремиться к конгруэнтности и признавать свои настоящие чувства»
Правильно: «Эти два силуэта конгруэнтны — один является зеркальным отражением другого»
Варламова Дарья
69 722
Конгруэнтность — Психологос
Конгруэнтность — согласованность и соразмерность элементов, образующих некоторое целое.
В практической психологии, конгруэнтность — согласованность тех или иных элементов жизни человека, в первую очередь соответствие внешнего выражения внутреннему содержанию.
В этом смысле говорят о конгруэнтности (или неконгруэнтности) вербальной или невербальной информации, конгруэнтности его слов и его дел, конгруэнтности его состояния и того, что он показывает окружающим, соответствия его жизненных ценностей и того, как человек живет в реальности.
Конгруэнтность — одно из проявлений аутентичности. «Конгруэнтность — когда ты живешь, говоришь и дышишь в соответствии с твоими ценностями и целями, с тем кто ты есть» — Лидия Маркович Росати. У человека все спокойно внутри, он спокоен внешне — налицо конгруэнтность. У человека не расходятся его слова и дела — это конгруэнтность. Соответствие того, что говорится, и того как говорится — это конгруэнтность.
С другой стороны, внутри у человека мандраж, а внешне он демонстрирует уверенность. Если вы это заметили, это его неконгруэнтность.
Или, учитель, объясняющий материал, спрашивает, понял ученик его или нет. Ученик может кивнуть в ответ «Понял», но тон его голоса или выражение глаз может заставить учителя усомниться в этом. Учитель видит неконгруэнтность.
Конгруэнтность — оценочное понятие, это всегда оценка извне и всегда интерпретация. Если вам кажется, что что-то в человеке не соответствует чему-то, вы можете говорить о неконгруэнтности. Хотя, возможно, это просто ваши проекции, интрепретации или просто неосведомленность. Прежде чем уличить другого человека в неконгруэнтности, имеет смысл поискать более позитивные интерпретации того, что вы наблюдаете.
Всякая ли конгруэнтность хороша?
Нет. Если человек имеет низкие ценности и согласованно с этим живет в режиме бардака или расхлябанности — он когруэнтен, но едва ли вы захотите долго быть с этим человеком рядом. Конгруэнтными бывают бандиты, но мало кого это радует.
Конгруэнтность иногда противоречит деловой эффективности. Конгруэнтность как право и необходимость выражать вовне неконтролируемые эмоции, особенно если это неуместно и никому не нужно, идет во вред делу.
Нужно ли, правильно ли во время выступления показывать свои страхи и неуверенность? Практика публичных выступлений говорит — нет, этого делать не следует.
Требование конгруэнтности не всегда соответствует житейским реалиям.
Ситуация: вокруг вас средневековье, вы живете в окружении инквизиции, и при этом ваши ценности отличаются от строго католических. Будет ли разумным и адекватным жить так, будто инквизиции не существует, жить конгруэнтно своим взглядам и ценностям? Едва ли вы осудите Коперника и Галилея, которые ради дела своей жизни иногда были осторожными и не полностью удовлетворяли требованиям конгруэнтности.
Конгруэнтность и развитие личности
Конгруэнтность может и должна быть целью развития личности, но в процессе развития требование конгруэнтности является скорее помехой. Развитие личности — всегда освоение новых форм поведения, не привычных и не характерных для нас прежних, и несоответствие себя прежнего и себя нарождающегося, себя нового — несоответствие естественное.
Человек хмурый учится улыбаться — вначале его улыбка будет неестетственной и натянутой. Это нормально, как этап роста. Важно дойти до уровня, когда ваша улыбка будет не внешней естественной, а станет выражением вашего внутренней радости и доброжелательности к людям.
Развитие начинается с неконгруэнтности, но должно конгруэнтностью завершиться.
Что такое Конгруэнтность? Определение, примеры, факты
Значение конгруэнтности
Если две фигуры можно расположить точно друг над другом, они называются конгруэнтными фигурами.
Если вы положите один ломтик хлеба на другой, вы обнаружите, что оба ломтика имеют одинаковую форму и размер.
Термин «конгруэнтный» означает в точности одинаковую форму и размер. Эта форма и размер должны оставаться одинаковыми, даже когда мы переворачиваем, поворачиваем или вращаем фигуры.
Примеры конгруэнтных фигур
Две бабочки одинаковой формы и размера
Два конфетных мороженых одинаковой формы и размера
Два кубика лего одинаковой формы и размера
Символ Конгруэнтности
Конгруэнтность представлена символом — ‘ ≅ ‘
Поскольку конгруэнтность объектов подразумевает одинаковую форму и размер; символ конгруэнтности состоит из двух символов, расположенных один над другим.
Есть символ тильда « » , что означает сходство по форме, и «=» , что означает равенство по размеру.
Следовательно, конгруэнтность представлена символом ‘ ≅ ‘
Если два объекта A и B конгруэнтны друг другу, мы запишем это как: A ≅ B
Congru ent Line Segments
Поскольку конгруэнтность подразумевает одинаковую форму и размер, отрезки будут конгруэнтны, если их форма и размер одинаковы.
Внимательно посмотрите на изображение выше.
Поскольку AB и PQ являются отрезками прямой, они имеют одинаковую форму. Длина отрезка AB равна 5 см и PQ также равна 5 см. Следовательно, длины обоих отрезков равны друг другу.
Итак, если две или более прямых равны по длине, говорят, что они конгруэнтны друг другу.
Следовательно, отрезки AB и PQ конгруэнтны друг другу.
Следовательно, он будет представлен в виде отрезка AB ≅ отрезка PQ.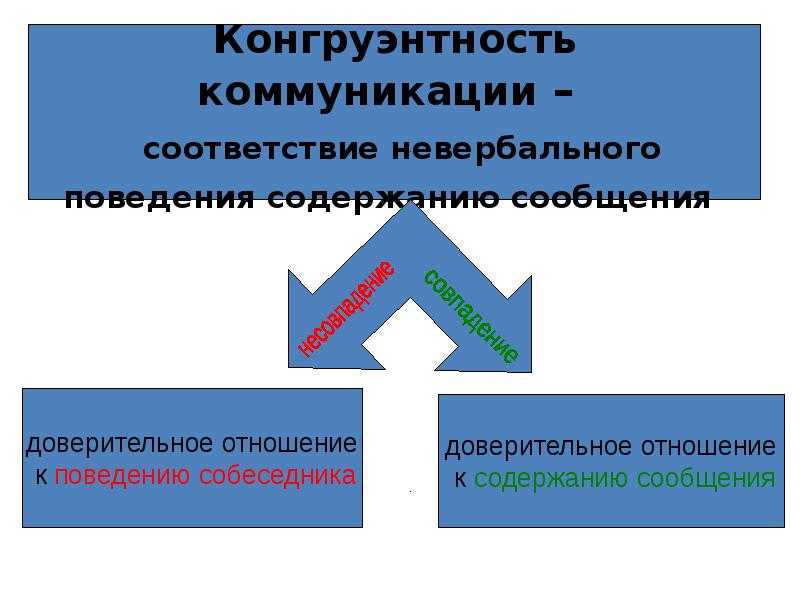
Конгруэнтные углы
На приведенной выше диаграмме ∠ ABC = 40 °, , тогда как ∠ PQR = 40 9 0013°.
Если мы наложим или перекроем ∠ ABC на ∠ PQR, мы обнаружим, что оба угла конгруэнтны друг другу.
Согласно правилу, два угла равны, если меры обоих углов равны друг другу.
Следовательно, ∠ ABC ≅ ∠ PQR
Конгруэнтные окружности
На приведенной выше диаграмме радиус окружности A представлен радиусом OR, тогда как радиус окружности B представлен OP.
Оба круга имеют одинаковую форму и одинаковый размер, так как длина радиусов OR и OP равна 2 см каждый.
Согласно условию конгруэнтности, если радиусы двух окружностей равны по длине, то обе окружности конгруэнтны друг другу. Это также означает, что оба круга можно легко разместить друг над другом.
Таким образом, окружность A конгруэнтна окружности B и может быть записана как окружность A ≅ окружность B.
Конгруэнтные треугольники
стороны и углы должны быть равны.
Заметим, что:
Сторона AC = EG, AB = EF и BC = FG,
и ∠ A = ∠ E, ∠ B = ∠ F и ∠ C = ∠ G
Следовательно, ABC ≅ EFG .
Всякий раз, когда два или более треугольника конгруэнтны, их соответствующие стороны и углы также конгруэнтны в соответствии с правилом соответствующих частей конгруэнтных треугольников (CPCT),
Разница между конгруэнтными фигурами и подобными фигурами
Существенная разница между конгруэнтными фигурами и подобными фигурами заключается в том, что:
| Конгруэнтные фигуры | |
| В двух конгруэнтных фигурах обе соответствующие углы и длины соответствующих сторон равны между собой. | На двух похожих фигурах формы выглядят одинаково. Это потому, что соответствующие углы равны. Однако длины соответствующих сторон не равны друг другу. |
Согласно приведенной выше диаграмме, конгруэнтные фигуры представлены ABC и DEF, тогда как аналогичные фигуры представлены MNO и XYZ
Что касается конгруэнтных фигур, EF,
∠ A = ∠ D, ∠ B = ∠ E и ∠ C = ∠ F
Следовательно, ABC ≅ DEF, так как соответствующие углы и длины соответствующих сторон равны друг другу.
Принимая во внимание, что в отношении аналогичных фигур.
Равны только углы, которые равны ∠ M = ∠ X, ∠ N = ∠ Y и ∠ O = ∠ Z.
Длины соответствующих сторон не равны друг другу.
Следовательно, MNO и XYZ подобны друг другу.
Однако они не конгруэнтны друг другу.
Решенные примеры
Пример 1. Два угла ∠ ABC и ∠ XYZ равны друг другу?
Решение:
Мера ∠ ABC = 40° и ∠ XYZ = 60°.
По правилу два угла равны, если величины обоих углов равны друг другу.
Мера ∠ ABC не равна мере ∠ XYZ.
Следовательно, ∠ ABC не конгруэнтно ∠ XYZ.
Пример 2: Два треугольника MNO и XYZ равны. Укажите соответствующие стороны и углы, которые будут равны.
Решение:
Дано, ∆MNO ≅ ∆XYZ
Согласно CPCT все три соответствующие стороны и углы конгруэнтных треугольников ∆MNO и ∆XYZ будут равны друг другу.
Следовательно,
MN = XY
NO = YZ
MO = XZ
Кроме того,
∠ M = ∠ X, ∠ N = ∠ Y и ∠ O = ∠ Z
Пример 3: Являются ли ниже фигуры похожи или конгруэнтны друг другу?
На приведенной выше диаграмме длина радиуса OL равна 2 см, тогда как OM равна 1 см.
Чтобы две окружности были конгруэнтны друг другу, длина радиуса обеих окружностей должна быть равна друг другу.
Следовательно, обе окружности подобны друг другу, но не конгруэнтны друг другу.
Заключение
Мы понимаем, что одинаковые формы и размеры называются конгруэнтными в геометрии.
В конгруэнтных фигурах форма и размер должны оставаться одинаковыми, когда мы переворачиваем, поворачиваем или даже вращаем фигуры. И в конгруэнтной форме две фигуры могут быть размещены друг над другом.
С помощью SplashLearn ваш ребенок может в увлекательной форме изучить эту главу с помощью решенных примеров. SplashLearn является лучшей и самой надежной платформой для каждого ребенка, чтобы укрепить основы математики вашего ребенка. Эта образовательная онлайн-платформа делает обучение легким и увлекательным для вашего ребенка.
CTA
Вы ищете образовательную и развлекательную онлайн-платформу? Вы хотите, чтобы ваш ребенок изучал и практиковал математику, развлекаясь? Тогда не ждите слишком долго!
Зарегистрируйтесь в SplashLearn и повысьте уверенность своего ребенка в изучении математики.
Практические задачи
1 Найдите неверный ответ в случае двух конгруэнтных фигур. Конгруэнтные фигуры равны по размеру Конгруэнтны фигуры могут накладываться друг на друга Конгруэнтны фигуры не равны по форме Конгруэнтны фигуры можно поворачивать Правильный ответ: Конгруэнтны фигуры не равны по форме 2 В случае двух конгруэнтных треугольников △ABC и △MNO, если угол A равен 55°, какова мера угла M, когда он соответствует углу A?65° 55° 40° Ничего из вышеперечисленного Правильный ответ: 55° 3 Если △ABC ≅ △PQR, то какой угол будет равен ∠ R?∠B ∠C ∠A Ничего из вышеперечисленного Правильный ответ: ∠C |
Часто задаваемые вопросы
Когда можно сказать, что две фигуры равны?
Две фигуры можно назвать конгруэнтными, если они имеют одинаковую форму и одинаковый размер.
Могут ли конгруэнтные фигуры быть разных размеров?
Нет, конгруэнтные фигуры не могут иметь разные размеры. Вместо этого фигуры называются конгруэнтными, если они имеют одинаковую форму и одинаковый размер. Фигуры одинаковой формы и разных размеров называются подобными.
Все ли конгруэнтные фигуры подобны?
Да, все конгруэнтные фигуры подобны.
Могут ли конгруэнтные формы или фигуры быть зеркальными отображениями?
Да, конгруэнтные фигуры можно рассматривать как зеркальные отражения, поскольку они имеют одинаковую форму и одинаковый размер.
Имеют ли конгруэнтные круги одинаковый диаметр?
Известно, что две окружности конгруэнтны, если их радиусы равны друг другу.
Длина диаметра в два раза больше радиуса. Следовательно, конгруэнтные окружности имеют одинаковый диаметр.
Могут ли звезды быть конгруэнтными?
Две звезды можно считать конгруэнтными только в том случае, если они обе имеют одинаковую форму и размер, даже если их перевернуть, повернуть или наложить друг на друга.
Конгруэнтность (конгруэнтность) — значение, определение, примеры
LearnPracticeDownload
В геометрии конгруэнтность означает идентичность по форме и размеру. Конгруэнтность может быть применена к отрезкам прямых, углам и фигурам. Любые два отрезка называются конгруэнтными, если они равны по длине. Два угла называются равными, если они равны. Два треугольника называются равными, если их соответствующие стороны и углы равны. Давайте узнаем больше о конгруэнтности и конгруэнтных фигурах в этой статье.
| 1. | Конгруэнтное значение в геометрии |
2. | Конгруэнтные фигуры |
| 3. | Конгруэнтные и подобные фигуры |
| 4. | Часто задаваемые вопросы о конгруэнтности |
Конгруэнтное значение в геометрии
Слово «конгруэнтный» означает «точно равный» по форме и размеру. Даже когда мы поворачиваем, переворачиваем или поворачиваем фигуры, они остаются одинаковыми. Например, нарисуйте два круга одинакового радиуса, затем вырежьте их и наложите друг на друга. Мы заметим, что они будут накладываться друг на друга, то есть располагаться полностью друг над другом. Это показывает, что две окружности конгруэнтны. Следующие окружности называются конгруэнтными, так как они имеют одинаковый радиус и могут располагаться точно друг над другом. Символ, который используется для обозначения соответствия цифр, — «≅». Поскольку окружность A конгруэнтна окружности B, мы можем выразить этот факт следующим образом: окружность A ≅ окружность B.
Конгруэнтные фигуры
Конгруэнтность любых двух фигур можно увидеть, если их можно расположить точно друг над другом. Слово «конгруэнтность» используется для выражения отношения двух фигур, которые считаются конгруэнтными. Другими словами, если любые две геометрические фигуры можно наложить друг на друга, они называются конгруэнтными фигурами. Это свойство применимо ко всем фигурам, таким как треугольники, четырехугольники и так далее. Помимо фигур, отрезки и углы также называются конгруэнтными, если они имеют одинаковую меру. Обратите внимание на следующий рисунок, чтобы понять, что означают конгруэнтные цифры.
Конгруэнтные и подобные фигуры
Существует разница между конгруэнтными и подобными фигурами. Конгруэнтные фигуры имеют одинаковые соответствующие длины сторон и соответствующие углы равны. Однако подобные фигуры могут иметь одинаковую форму, но их размер может быть разным.
Например, обратите внимание на следующие треугольники, которые показывают разницу между конгруэнтными и подобными фигурами.
На конгруэнтных фигурах видно, что все соответствующие стороны и углы равны. Однако, если мы обратим внимание на подобные фигуры, мы увидим, что соответствующие углы равновелики, но стороны не равной длины.
Конгруэнтность треугольников
Два треугольника называются конгруэнтными, если их стороны равны по длине, углы равны и их можно наложить друг на друга.
На приведенном выше рисунке треугольники Δ ABC и Δ PQR равны. Это означает, что соответствующие углы и соответствующие стороны в обоих треугольниках равны.
Стороны: AB = PQ, BC = QR и AC = PR;
Углы: ∠A = ∠P, ∠B = ∠Q и ∠C = ∠R.
Следовательно, Δ ABC ≅ Δ PQR
Ниже приведены теоремы о конгруэнтности или критерии конгруэнтности треугольников, которые помогают доказать конгруэнтность треугольников.
- SSS (боковой, боковой, боковой)
- SAS (боковой, угловой, боковой)
- ASA (угол, сторона, угол)
- AAS (угол, угол, сторона)
- RHS (прямой угол-гипотенуза-сторона или теорема о катете гипотенузы)
Ссылки по теме
Ознакомьтесь со следующими страницами, посвященными конгруэнтности и конгруэнтным фигурам.
- Свойства треугольника
- Треугольники
- Равные углы
- Конгруэнтность треугольников
- ССС Формула
- Соответствующие углы
- САС
Конгруэнтные примеры
Пример 1: Два четырехугольника, показанные ниже, конгруэнтны . Какой угол в четырехугольнике PQRS соответствует углу ∠WXY в четырехугольнике WXYZ?
Решение:
Отождествим соответствующие части в обоих четырехугольниках.
∠WXY отмечен четырьмя дугами в четырехугольнике WXYZ.
∠QRS также отмечен четырьмя дугами в четырехугольнике PQRS. Это показывает, что они равны, что означает, что ∠QRS совпадает с ∠WXY. Следовательно, ∠WXY соответствует ∠QRS.Пример 2. У Эммы есть четыре квадрата со следующими длинами сторон: Квадрат A, сторона = 5 дюймов, Квадрат B, сторона = 7 дюймов, Квадрат C, сторона = 5 дюймов, Квадрат D, сторона = 8 дюймов.
Ей нужны два квадрата, которые можно расположить ровно один над другим. Поможешь ей выбрать конгруэнтные квадраты? Решение: Квадраты с одинаковыми сторонами будут накладываться друг на друга, потому что они конгруэнтны. Итак, Эмма должна найти два квадрата, у которых длины сторон абсолютно одинаковы. В приведенном списке мы видим, что стороны квадрата A и квадрата C имеют одинаковую длину, то есть 5 дюймов. Таким образом, Эмма может выбрать квадраты A и C, потому что их можно расположить точно друг над другом.
Ей нужны два квадрата, которые можно расположить ровно один над другим. Поможешь ей выбрать конгруэнтные квадраты? перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Congruent
Что такое конгруэнтные фигуры?
Конгруэнтные фигуры — это фигуры, у которых стороны одинаковой длины и углы одинаковой величины.
Другими словами, когда одна фигура накладывается на другую, фигуры называются конгруэнтными фигурами. Они точно подходят друг к другу, даже когда их поворачивают или переворачивают.
Как доказать, что треугольники конгруэнтны?
Два треугольника называются конгруэнтными, если их соответствующие стороны равны по длине и их соответствующие углы равны по размеру.
Каковы свойства конгруэнтности?
Свойства конгруэнтности применимы к линиям, углам и фигурам. Их можно перечислить следующим образом: рефлексивное свойство, симметричное свойство и транзитивное свойство.
- Рефлексивное свойство конгруэнтности говорит о том, что отрезок, угол или фигура всегда конгруэнтны сами себе. Например, ∠P≅∠P
- Свойство симметрии гласит, что если одна фигура конгруэнтна другой, то и вторая конгруэнтна первой. Для любых двух углов P и Q, если ∠P ≅∠Q, то ∠Q ≅∠P.
- Транзитивное свойство конгруэнтности утверждает, что если прямая 1 конгруэнтна прямой 2, а прямая 2 конгруэнтна прямой 3, то прямая 1 также конгруэнтна прямой 3.
У какой фигуры все стороны равны?
Квадрат — единственная фигура, у которой все стороны равны и все углы равны.
Каковы 5 критериев соответствия треугольников?
В следующем списке показаны критерии равенства треугольников или теоремы, доказывающие сходство треугольников.
- SSS (боковой, боковой, боковой)
- SAS (боковой, угол, боковой)
- ASA (угол, сторона, угол)
- AAS (угол, угол, сторона)
- RHS (прямой угол-гипотенуза-сторона или теорема о катете гипотенузы)
Всегда ли вертикальные углы равны?
Да, вертикальные углы всегда конгруэнтны, потому что согласно теореме о вертикальных углах, когда две прямые пересекаются друг с другом, образующиеся противоположные углы всегда равны (конгруэнтны). Эти углы называются вертикально противоположными углами или вертикальными углами.
Какое другое слово для конгруэнтного?
Конгруэнтные означает «идентичные» по форме и размеру.