Ассоциативный ряд: примеры, инструмент психолога
В самом обобщенном понимании, ассоциативный ряд – это набор элементов, связанных друг с другом по какому-либо общему признаку. Причем, если элемент А связан с элементом Б по какому-либо ассоциированному признаку, а элемент Б связан с элементом С, необязательно, чтобы в ассоциативном ряду А было связано С. Например, при упоминании слова «лето» может возникнуть следующий ассоциативный ряд: море, пляж, песок и т.д. Каждое последующее слово связано с предыдущим, но необязательно с тем, которое стоит перед предыдущим. Это последовательный ассоциативный ряд. Есть также ряды, у которых все элементы объединены одним общим признаком. Более подробно этот вопрос разбирается в теории множеств.
Ассоциативные ряды сейчас нашли широкое применение в самых разных областях гуманитарного знания. С помощью тестирования на ассоциации можно понять психологическое состояние респондента, его жизненные взгляды и даже особенности мышления. Для этого проводится так называемый ассоциативный эксперимент, в ходе которого предлагается выбирать предметы или называть слова, ассоциирующиеся с некоторыми эталонными.
К ассоциативным экспериментам относится известный цветовой тест Люшера, так как тяга к той или иной цветовой палитре связана с проекцией на нее внутренних состояний человека.
Тем не менее, стоит подчеркнуть, что оценка личности по ассоциативным схемам не всегда адекватна. Каждый человек может назвать свой собственный ассоциативный ряд к любому слову, потому что ассоциативные связи формируются в процессе приобретения опыта. У каждого он свой. Но нормальные с психологической точки зрения люди будут иметь похожие ассоциативные ряды. А вот одним из главных признаков шизофрении как раз является наличие диссоциативного мышления.
Более оправдано использование ассоциативного эксперимента при оценке развития дошкольников и детей младшего школьного возраста. Для обучения детей сейчас нередко используются так называемые ассоциативные игры, когда необходимо рассортировать несколько предметов по определенному признаку или находить по общему признаку пары.
Ассоциативный ряд применяется также при оценке уровня эрудиции индивидуума и при тестах на IQ.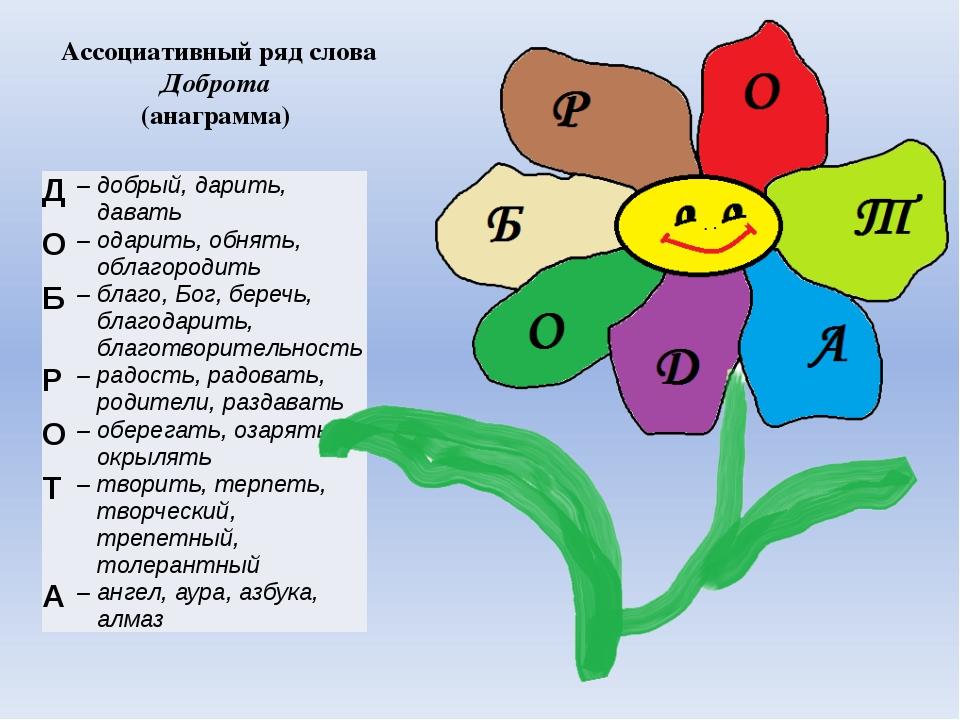
Несмотря на широкое распространение именно этого вида оценки интеллектуальных способностей, он все же имеет некоторые недостатки. Дело в том, что в одном случае индивидуум может выстроить правильный ассоциативный ряд или объединить объекты по общему признаку в процессе размышлений, а в другом – как следствие предыдущего опыта. Соответственно, в первом случае мы будем иметь дело с более способным в мыслительно-логическом плане человеком, а во втором – с более эрудированным и натренированным.
Впрочем, некоторые исследователи считают, что способность быстро структурировать информацию и находить в ней логические связи всегда является следствием натренированного мыслительно-логического аппарата. Тренировка же должна начинаться как можно раньше, в детстве, и проводиться на самом широком спектре задач.
Ассоциативный ряд как инструмент психолога
В самом обобщенном понимании, ассоциативный ряд – это набор элементов, связанных друг с другом по какому-либо общему признаку. Причем, если элемент А связан с элементом Б по какому-либо ассоциированному признаку, а элемент Б связан с элементом С, необязательно, чтобы в ассоциативном ряду А было связано С.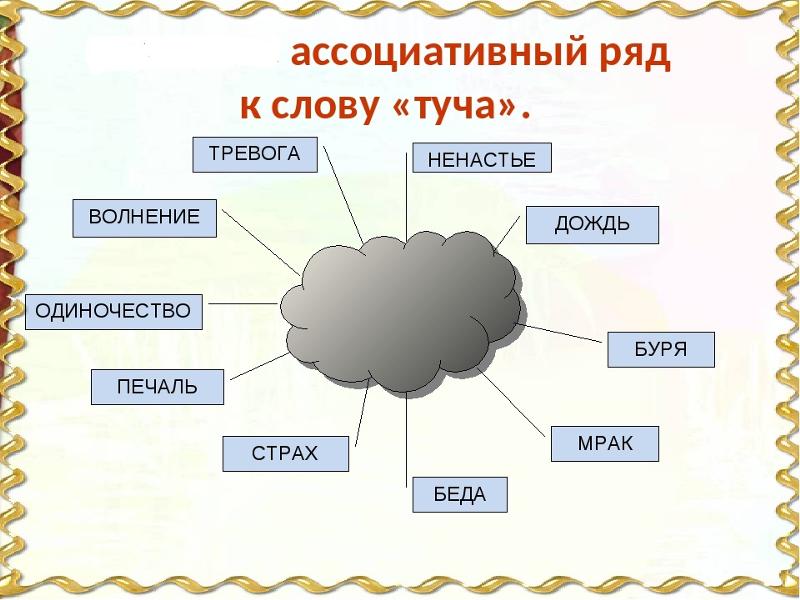
Например, при упоминании слова «лето» может возникнуть следующий ассоциативный ряд: море, пляж, песок и т.д. Каждое последующее слово связано с предыдущим, но необязательно с тем, которое стоит перед предыдущим. Это последовательный ассоциативный ряд. Есть также ряды, у которых все элементы объединены одним общим признаком. Более подробно этот вопрос разбирается в теории множеств.
Ассоциативные ряды сейчас нашли широкое применение в самых разных областях гуманитарного знания. С помощью тестирования на ассоциации можно понять психологическое состояние респондента, его жизненные взгляды и даже особенности мышления. Для этого проводится так называемый ассоциативный эксперимент, в ходе которого предлагается выбирать предметы или называть слова, ассоциирующиеся с некоторыми эталонными. К ассоциативным экспериментам относится известный цветовой тест Люшера, так как тяга к той или иной цветовой палитре связана с проекцией на нее внутренних состояний человека.
Тем не менее, стоит подчеркнуть, что оценка личности по ассоциативным схемам не всегда адекватна. Каждый человек может назвать свой собственный ассоциативный ряд к любому слову, потому что ассоциативные связи формируются в процессе приобретения опыта. У каждого он свой. Но нормальные с психологической точки зрения люди будут иметь похожие ассоциативные ряды. А вот одним из главных признаков шизофрении как раз является наличие диссоциативного мышления.
Более оправдано использование ассоциативного эксперимента при оценке развития дошкольников и детей младшего школьного возраста. Для обучения детей сейчас нередко используются так называемые ассоциативные игры, когда необходимо рассортировать несколько предметов по определенному признаку или находить по общему признаку пары.
Ассоциативный ряд применяется также при оценке уровня эрудиции индивидуума и при тестах на IQ. Несмотря на широкое распространение именно этого вида оценки интеллектуальных способностей, он все же имеет некоторые недостатки.
Дело в том, что в одном случае индивидуум может выстроить правильный ассоциативный ряд или объединить объекты по общему признаку в процессе размышлений, а в другом – как следствие предыдущего опыта. Соответственно, в первом случае мы будем иметь дело с более способным в мыслительно-логическом плане человеком, а во втором – с более эрудированным и натренированным.
Впрочем, некоторые исследователи считают, что способность быстро структурировать информацию и находить в ней логические связи всегда является следствием натренированного мыслительно-логического аппарата. Тренировка же должна начинаться как можно раньше, в детстве, и проводиться на самом широком спектре задач.
реальный анализ — Докажите, что если бесконечный ряд сходится, то выполняется ассоциативное свойство
спросил
Изменено 8 лет, 2 месяца назад
Просмотрено 5к раз
$\begingroup$
Я занимаюсь самостоятельным изучением книги Стивена Эбботта «Понимание анализа» и понятия не имею, как выполнять упражнение 2.
5.2 на стр. 57.
Упражнение выглядит следующим образом:
Докажите, что если бесконечный ряд сходится, то выполняется свойство ассоциативности. Предположим, что $a_1+a_2 + a_3+a_4 + a_5+\cdots$ сходится к пределу $L$ (т. е. последовательность частичных сумм $(s_n) \to L$). [Это предложение уже сбивает меня с толку; Я не понимаю, почему если $(a_n) \to L$, то отсюда следует, что $(s_n) \to L$?] Покажите, что любая перегруппировка термов $$ (a_1 + a_2 + \cdots + a_{n_1}) + (a_{n_1+1} + \cdots + a_{n_2}) + (a_{n_2 + 1} + \cdots + a_{n_3}) + \cdots $$ приводит к ряду, который также сходится к $L$.
Теперь я знаю, что лучше всего показать, что я пробовал до сих пор, но я понятия не имею, с чего начать. Любое понимание очень ценится.
- реальный анализ
- последовательности-и-ряды
- конвергенция-дивергенция
$\endgroup$
2
$\begingroup$
Для вашего первого замешательства $a_1 + a_2 + a_3+\cdots$ сходится к пределу $L$ — это всего лишь $\lim_{n\to \infty}s_n = L$ по определению.
Это не означает, что $\lim_{n\to \infty}a_n = L$.
Тогда, чтобы ответить на вопрос, $\lim_{n\to \infty}s_n = L$ означает $\forall \epsilon >
0$, существует $N$ такое, что для всех $n > N$ имеем $ |s_n — L |< \epsilon$.Обозначим
$b_1 = (a_1 + a_2 + \cdots + a_{n_1})$
$b_2 = (a_1 + a_2 + \cdots + a_{n_1}) + (a_{n_1+1} + \ cdots + a_{n_2})$ $b_3 = (a_1 + a_2 + \cdots + a_{n_1}) + (a_{n_1+1} + \cdots + a_{n_2}) + (a_{n_2 + 1} + \cdots + a_{n_3}) $
Тогда у вас есть $b_k = s_{n_k}$ для некоторого $n_k$ не меньше, чем $k$. Итак, если $k>N$, $n_k \geq k >N$, то $|b_k-L| = |s_{n_k}-L| < \эпсилон$.
По определению мы доказали, что $b_k$ сходится к $L$
$\endgroup$
$\begingroup$
путем введения последовательности $(n_k)_k$, которая является извлечением последовательности $(n)_n$, доказательство легко: теперь мы имеем $s_{n_k}=(a_1+\ldots+a_{n_1})+ \ldots+(a_{n_1+1}+\ldots+a_{n_k})$, поскольку $s_n\to L$ затем $s_{n_k}\to L$ ($s_{n_k}$ — извлечение $(s_n )$).
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
реальный анализ — Ассоциативность бесконечных рядов
Задавать вопрос
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 91 раз
$\begingroup$
В моих заметках по вычислениям мой профессор представил следующее утверждение: 9{\infty}a_n$$
Предполагается, что это предложение говорит о том, что если бесконечный ряд сходится, то выполняется свойство ассоциативности. Я читал эквивалентное предложение, но записанное по-другому, и смог доказать его. Однако я не могу доказать утверждение так, как его написал мой профессор. Приветствуется любая помощь
Приложение: Утверждение, которое мне удалось доказать, — это Упражнение 2.